(本题满分14分)数列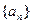 的前
的前 项和为
项和为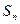 ,且
,且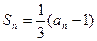
(1)求  ,
, 及
及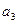 ;
;
(2)证明:数列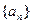 是等比数列,并求
是等比数列,并求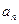 .
.
(本题满分12分)△ABC中,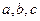 是A,B,C所
是A,B,C所 对的边,S是
对的边,S是 该三角形的面积,且
该三角形的面积,且

( 1)求∠B的大小;
1)求∠B的大小;
(2)若 =4,
=4, ,求
,求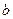
 的值。
的值。
(本题满分12分)已知三角形ABC的顶点坐标为A(-1,5)、B(-2,-1)、C(4, 3),M是BC边上的中点。
3),M是BC边上的中点。
(1)求AB边所在的直线方程;
(2)求中线AM的长。
(本题满分12分)作图(不要求写出作法,请保留作图痕迹)
(1)画出下图几何体的三视图(尺寸自定);
(2)画出一个底面直径为4cm,高为2cm的圆锥的直观图
(本题满分14分) 设数列
设数列 的前
的前 项和为
项和为 ,且
,且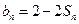 ;数列
;数列 为等差数列,且
为等差数列,且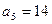 ,
, .
.
(1) 求数列 的通项公式;
的通项公式;
(2) 若 ,
, 为数列
为数列 的前
的前 项和. 求证:
项和. 求证: .
.