在高中“自选模块”考试中，某考场的每位同学都选了一道数学题，第一小组选《数学史与不等式选讲》的有1人，选《矩阵变换和坐标系与参数方程》的有5人，第二小组选《数学史与不等式选讲》的有2人，选《矩阵变换和坐标系与参数方程》的有4人，现从第一、第二两小组各任选2人分析得分情况
（1）求选出的4 人均为选《矩阵变换和坐标系与参数方程》的概率；
（2）设
为选出的4个人中选《数学史与不等式选讲》的人数，求的分布列和数学期望
已知f（x）是定义在（0，+∞）上的增函数，且满足f（xy）＝f（x）＋f（y），f（2）＝1.
（1）求证：f（8）＝3
（2）求不等式f（x）－f（x－2）>3的解集.
已知奇函数f（x）=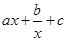
（a、b、c是常数），且满足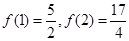
（1）求a、b、c的值
（2）试判断函数f（x）在区间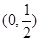
上的单调性并证明
已知函数f（x）是定义在R上的奇函数，当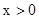
时，
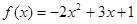求：
（1）当x<0时，f（x）的解析式
（2）f（x）在R上的解析式
已知集合A＝{x|x2－5x＋6＝0}，B＝{x|x2＋ax＋6＝0}，且B⊆A，求实数a的取值范围．
已知全集U为R，集合A＝{x|0<x≤2}，B＝{x|x<－3或x>1}．
求：（1）A∩B；（2）（∁UA）∩（∁UB）；（3）∁U（A∪B）．