如图1,在直角梯形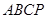 中,
中, ,
,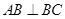 ,
,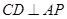 ,
,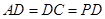 ,
,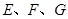 分别是
分别是 的中点,现将
的中点,现将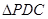 沿
沿 折起,使平面
折起,使平面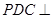 平面
平面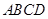 (如图2),且所得到的四棱锥
(如图2),且所得到的四棱锥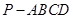 的正视图、侧视图、俯视图的面积总和为8.
的正视图、侧视图、俯视图的面积总和为8.
⑴求点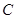 到平面
到平面 的距离;
的距离;
⑵求二面角 的大小的夹角的余弦值;
的大小的夹角的余弦值;
⑶在线段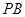 上确定一点
上确定一点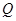 ,使
,使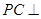 平面
平面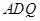 ,并给出证明过程.
,并给出证明过程.
在一个花瓶中装有6枝鲜花,其中3枝山茶花,2枝杜鹃花和1枝君子兰,从中任取2枝鲜花.
(1)求恰有一枝山茶花的概率;
(2)求没有君子兰的概率.
如图,在长方体 中,
中, ,点
,点 是棱
是棱 上的一个动点.
上的一个动点.
(1)证明: ;
;
(2)当 为
为 的中点时,求点
的中点时,求点 到面
到面 的距离;
的距离;
(3)线段 的长为何值时,二面角
的长为何值时,二面角 的大小为
的大小为 .
.
某班同学利用寒假进行社会实践,对年龄在 的人群随机抽取
的人群随机抽取 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:

(1)补全频率分布直方图,并求 的值;
的值;
(2)从年龄在 的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在
的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在 的概率.
的概率.
如图,在矩形 中,点
中,点 为边
为边 上的点,点
上的点,点 为边
为边 的中点,
的中点, ,现将
,现将 沿
沿 边折至
边折至 位置,且平面
位置,且平面 平面
平面 .
.
(1) 求证:平面 平面
平面 ;
;
(2) 求二面角 的大小.
的大小.
已知二次函数
 (
( ),若
),若 是从区间
是从区间 中随机抽取的一个数,
中随机抽取的一个数, 是从区间
是从区间 中随机抽取的一个数,求方程
中随机抽取的一个数,求方程 没有实数根的概率.
没有实数根的概率.