数列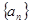 中,
中,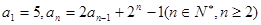 ,若存在实数
,若存在实数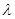 ,使得数列
,使得数列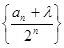 为等差数列,则
为等差数列,则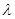 =
=
下列五个命题:
①函数y=tan(-)的对称中心是(2kπ+,0)(k∈Z).
②终边在y轴上的角的集合是{α|α=,k∈Z}.
③在同一坐标系中,函数y=sinx的图像和函数y=x的图像有三个公共点.
④把函数y=3sin(2x+)的图像向右平移得到y=3sin2x的图像.
⑤函数y=sin(x-)在[0,π]上是减少的.
其中,正确命题的序号是__________.(写出所有正确命题的序号)
若角α的终边落在直线x+y=0上,则+的值等于__________;,则+的值等于__________;
若样本数据 的平均数是10,则对于样本数据
的平均数是10,则对于样本数据
 ,平均数为 ____________;
,平均数为 ____________;
一般情况下,年龄在18至38岁的人们,其体重y(kg)对身高x(cm)的回归方程为y=0.7x-52,李明同学身高为180cm,那么他的体重估计为 ___kg.