（本小题满分13分）
椭圆C：
的离心率为
，且过点（2,0）
（1）求椭圆C的方程；
（2）设直线
：
与椭圆C交于A、B两点，O为坐标原点，若
OAB为直角三角形，求
的值。
如图，在五棱锥P—ABCDE中，PA⊥平面ABCDE，AB∥CD，AC∥ED，AE∥BC，
ABC=45°，AB=2
，BC=2AE=4，三角形PAB是等腰三角形．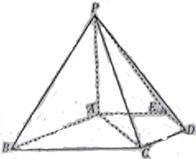
（Ⅰ）求证
：平面PCD⊥平面PAC；
（Ⅱ）求直线PB与平面PCD所成角的大小；
（Ⅲ）求四棱锥
P—ACDE的体积．
已知等差数列
满足：
，
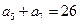，的前n项和为
．
（Ⅰ）求
及；
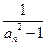（Ⅱ）令bn=
(n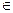
N*)，求数列
的前n项和
．
已知函数
，其图象过点（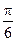
,
）．
（Ⅰ）求
的值；
（Ⅱ）将函数
的图象上各点的横坐标缩短到原来的，纵坐标不变，得到函数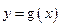
的图象，求函数
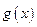在[0, 
]上的最大值和最小值．
解不等式 
选修4—4坐标系与参数方程。
在极坐标系中，方程
和
的直角坐标方程是什么？并求它们交点的极坐标？