倾角 的粗糙斜面位于水平地面上,质量
的粗糙斜面位于水平地面上,质量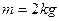 的木块置于斜面顶端,从静止开始匀加速下滑,经
的木块置于斜面顶端,从静止开始匀加速下滑,经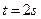 到达底端,运动路程L=4
到达底端,运动路程L=4 ,在此过程中斜面保持静止(
,在此过程中斜面保持静止(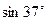 =0.6,
=0.6,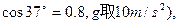 求:
求:
(1)求木块对斜面的压力大小和摩擦力大小;
(2)地面对斜面的支持力大小与摩擦力大小;
(3)通过计算证明木块在此过程中满足动能定理。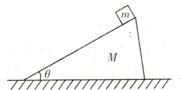
如图所示,质量为m,边长为L的正方形线框,在有界匀强磁场上方h高处由静止自由下落,线框的总电阻为R,磁感应强度为B的匀强磁场宽度为2L.线框下落过程中,ab边始终与磁场边界平行且处于水平方向.已知ab边刚穿出磁场下界时线框恰好做匀速运动.求: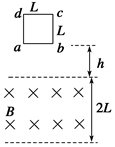
(1)ab边刚穿出磁场下界时速度;
(2)cd边刚进入磁场上界时线框的速度;
(3)线框在整个穿过磁场的过程中,产生的焦耳热
交流发电机的发电原理是矩形线圈在匀强磁场中绕垂直于磁场的轴OO’匀速转动。一小型发电机的线圈共220匝,线圈面积S =0.05m2,线圈转动的频率为50Hz,线圈内阻不计,磁场的磁感应强度B ="" T。为用此发电机所发出交流电带动两个标有“220V 11kW”的电机正常工作,需在发电机的输出端a、b与电机之间接一个理想变压器,电路如图。求:
(1)发电机的输出电压为多少?
(2)变压器原副线圈的匝数比为多少?
(3)与变压器原线圈串联的交流电流表的示数为多少?
如图所示,在磁感强度为0.5T的匀强磁场中,让长0.2 m、电阻为1Ω的导体棒AB在光滑且足够长的金属框上以5m/s的速度向右匀速滑动。如果R1=R2=2Ω,其他导线上的电阻忽略不计。则: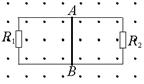
(1)导体AB两端的电势哪端高?及AB两端的电压是多大?
(2)在1min内,导体棒AB所产生的焦耳热为多少?
某小型水电站输出功率是20KW,输电线路总电阻是6Ω。 若采用5000v高压输电,输电线上的损耗电压为多少?输电线路损耗功率为多少?
如图所示,在光滑的水平地面上有一块长木板,其左端固定一挡板,挡板和长木板的总质量为m1 =3kg,其右端放一质量为m2= 1kg的小滑块,长木板的右端到挡板的距离为L=lm,整个装置处于静止状态。现对小滑块施加一水平拉力,将它拉到长木板的正中央时立即撤去拉力,此过程中拉力做功W=20J。此后小滑块与挡板碰撞(碰撞过程无机械能损失,碰撞时间极短),最终小滑块恰好未从长木板上掉下来。在小滑块与长木板发生相对运动的整个过程中,系统因摩擦产生热量Q= 12J。求
(1) 小滑块最终的速度大小;
(2) 碰撞结束时,小滑块与长木板的速度;
(3) 在小滑块与长木板发生相对运动的整个过程中,小滑块运动的位移大小。