(本小题12分)如图,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,E是MN的中点。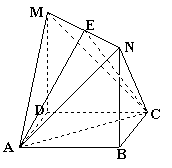
(1)求证:平面AEC ⊥平面AMN;
⊥平面AMN;
(2)求二面角M-AC-N的余弦值。
在数列{an}中,a1= ,an+1=
,an+1=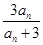 ,求a2、a3、a4的值,由此猜想数列{an}的通项公式,并用数学归纳法证明你的猜想.
,求a2、a3、a4的值,由此猜想数列{an}的通项公式,并用数学归纳法证明你的猜想.
有6名男医生,4名女医生.
(1)选3名男医生,2名女医生,让这5名医生到5个不同地区去巡回医疗,共有多少种不同方法?
(2)把10名医生分成两组,每组5人且每组都要有女医生,则有多少种不同分法?若将这两组医生分派到两地去,并且每组选出正副组长两人,又有多少种不同方案?
复数 ,若
,若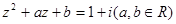 ,求
,求 的值.
的值.
设 和
和 是函数
是函数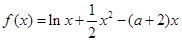 的两个极值点,其中
的两个极值点,其中 ,
, .
.
(1)若曲线 在点
在点 处的切线垂直于
处的切线垂直于 轴,求实数
轴,求实数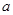 的值;
的值;
(2)求 的取值范围;
的取值范围;
(3)若 ,求
,求 的最大值(
的最大值( 是自然对数的底数).
是自然对数的底数).
已知函数 是定义在
是定义在 上的奇函数.当
上的奇函数.当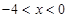 时,
时, ,且图象过点
,且图象过点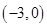 与点
与点 .
.
(Ⅰ)求实数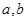 的值,并求函数
的值,并求函数 的解析式;
的解析式;
(Ⅱ)若关于 的方程
的方程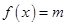 有两个不同的实数解,请写出实数
有两个不同的实数解,请写出实数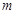 的取值范围;
的取值范围;
(Ⅲ)解关于 的不等式
的不等式 ,写出解集.
,写出解集.