如图,椭圆长轴端点为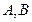 ,
,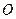 为椭圆中心,
为椭圆中心,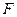 为椭圆的右焦点,且
为椭圆的右焦点,且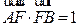 ,
,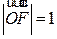 ;
;
(1)求椭圆的标准方程;
(2)记椭圆的上顶点为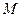 ,直线
,直线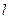 交椭圆于
交椭圆于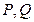 两点,问:是否存在直线
两点,问:是否存在直线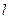 ,使点
,使点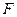 恰为
恰为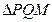 的垂心?若存在,求出直线
的垂心?若存在,求出直线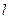 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.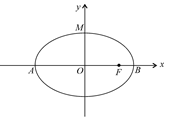
已知函数f(x)=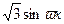 +
+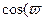 x+
x+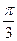 )+cos(
)+cos(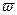 x
x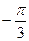 ),x
),x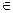 R,
R,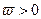
(1)求函数f(x)的值域;(2)若函数f(x)的最小正周期为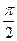 ,则当x
,则当x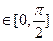 时,求f(x)的单调递减区间。
时,求f(x)的单调递减区间。
已知函数 ,
,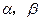 是方程
是方程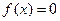 的两个根
的两个根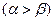 ,
,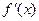 是
是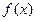 的导数.设
的导数.设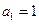 ,
,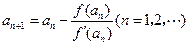 .
.
(1)求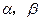 的值;
的值;
(2)已知对任意的正整数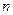 有
有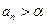 ,记
,记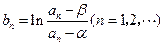 .求数列
.求数列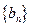 的前
的前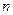 项和
项和 .
.
已知函数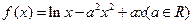 .
.
(1)当a=1时,证明函数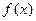 只有一个零点;
只有一个零点;
(2)若函数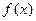 在区间(1,+∞)上是减函数,求实数a的取值范围.
在区间(1,+∞)上是减函数,求实数a的取值范围.
已知数列 的各项均为正数,它的前n项和Sn满足
的各项均为正数,它的前n项和Sn满足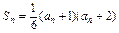 ,并且
,并且 成等比数列.
成等比数列.
(I)求数列 的通项公式;
的通项公式;
(II)设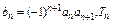 为数列
为数列 的前n项和,求
的前n项和,求 .
.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=6,BD=8,E是PB上任意一点,△AEC面积的最小值是3.
(Ⅰ)求证:AC⊥DE;
(Ⅱ)求四棱锥P-ABCD的体积.