下图为可测定比荷的某装置的简化示意图，在第一象限区域内有垂直于纸面向里的匀强磁场，磁感应强度大小B=2．0×10-3T,在X轴上距坐标原点L=0．50m的P处为离子的入射口，在Y上安放接收器，现将一带正电荷的粒子以v=3．5×104m/s的速率从P处射入磁场，若粒子在y轴上距坐标原点L=0．50m的M处被观测到，且运动轨迹半径恰好最小，设带电粒子
的质量为m,电量为q,不记其重力。
（1）求上述粒子的比荷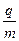
；
（2）如果在上述粒子运动过程中的某个时刻，在第一象限内再加一个匀强电场，就可以使其沿y轴正方向做匀速直线运动，求匀强电场的场强大小和方向，并求出从粒子射入磁场开始计时经过多长时间加这个匀强电场；
（3）为了在M处观测到按题设条件运动的上述粒子，在第一象限内的磁场可以局限在一个矩形区域内，求此矩形磁场区域的最小面积，并在图中画出该矩形。
如图所示,一圆桶形锅炉横卧于耐火材料砌成的底座上,已知锅炉半径R=lm,底座间L=1.6m,锅炉和内盛水的总重为2.4×104N,不计摩擦,求锅炉对底座的其中一侧的压力大小.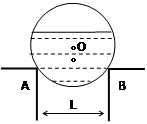
如图所示，在国庆阅兵演习中，某直升飞机在地面上空某高度A位置处于静止状态待命，接上级命令，要求该机10时58分20秒由静止状态沿水平方向作匀加速直线运动，经过AB段加速后，进入BC段的匀速受阅区，11时准时通过C位置，已知SAB=1km，SBC=2km。问：（1）直升飞机在BC段的速度大小是多少？ (2）直升飞机在AB段做匀加速直线运动时的加速度大小是多少？
一火车以2m/s的初速度，0.5m/s2的加速度做匀加速直线运动，求：（1）火车在第3 s末的速度是多少？（2）在前4 s的平均速度是多少？（3）在第5 s内的位移是多少？①3.5m/s②4m/s③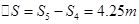
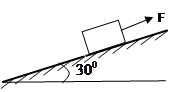
（10）质量为4Kg的物体放在与水平面成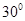
角，逐够长的粗糙斜面底端，物体与斜面间的动摩擦因素
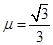，作用在物体上的外力与斜面平行，随时间变化的图象如图18所示，外力作用在物体上的时间共10秒，根据所给条件（
、
）
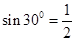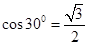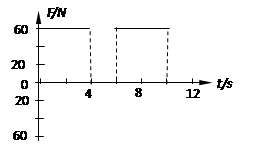
求：（1）物体所受的摩擦阻力为多大？（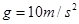
）
（2）物体在0—4秒内的加速度为多少？运动的位移为多少？
（3）物体从运动到停止时物体走过的总位移为多少
（4）如果前4秒F是水平作用在物体上，物体如何运动？
将一个重物用弹簧秤竖直悬挂起来后，弹簧秤的示数如图A所示(弹簧秤的量程100N)，之后将该物体放到粗糙的水平面上如图17B所示，当逐渐增大拉力到43N时，物体刚好运动，物体运动之后只用40N的拉力就能保持向右匀速运动（
）。求：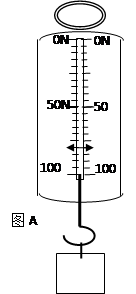
（1）物体的质量为多少千克？物体与地面的最大静摩擦力为多大？
（2）物体与地面间的动摩擦因素为多大?
（3）如果将拉力改为60N，并且由静止拉物体运动，经过时间为10秒时物体的运动速度和位移各为多少？