如图为某探究活动小组设计的节能运输系统,斜面轨道倾角为30°,质量为M的木箱与轨道的动摩擦因数为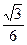 。木箱在轨道顶点时,自动装置将质量为m的货物装入木箱,然后木箱载着货物沿轨道无初速度滑下,当轻弹簧被压缩至最短时,自动卸货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端。再重复上述过程。求:(1)
。木箱在轨道顶点时,自动装置将质量为m的货物装入木箱,然后木箱载着货物沿轨道无初速度滑下,当轻弹簧被压缩至最短时,自动卸货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端。再重复上述过程。求:(1)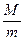 =?
=?
(2)在满足(1)的条件下,若物体下滑的最大距离为L, 则弹簧的最大弹性势能为多大?
则弹簧的最大弹性势能为多大?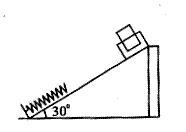
2008年北京奥运会上,我国运动员何雯娜在女子蹦床比赛中以37.80分的优异成绩夺得冠军。假设运动员表演时仅在竖直方向运动,通过传感器将弹簧床面与运动员间的弹力随时间变化的规律在计算机上绘制出如图所示的曲线,取 ,依据图象给出信息,判断下列物理量能否求出,如能求出写出必要的运算过程和最后结果。
,依据图象给出信息,判断下列物理量能否求出,如能求出写出必要的运算过程和最后结果。
⑴运动员的质量;
⑵运动过程中,运动员离开弹簧床上升的最大高度;
⑶运动过程中,运动员的最大加速度
如图所示,ABC为一固定在竖直平面内的光滑轨道,BC段水平,AB段与BC段平滑连接。质量为m的小球从高为h处由静止开始沿轨道下滑,与静止在轨道BC段上质量为km的小球发生碰撞,碰撞前后两小球的运动方向处于同一水平线上。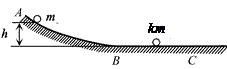
(1)若两小球碰撞后粘连在一起,求碰后它们的共同速度;
(2)若两小球在碰撞过程中无机械能损失,
a.为使两小球能发生第二次碰撞,求k应满足的条件;
b.为使两小球仅能发生两次碰撞,求k应满足的条件。
如图所示为某种质谱仪的结构示意图。其中加速电场的电压为U,静电分析器中与圆心O1等距各点的电场强度大小相同,方向沿径向指向圆心O1。磁分析器中以O2为圆心、圆心角为90°的扇形区域内,分布着方向垂直于纸面的匀强磁场,其左边界与静电分析器的右边界平行。由离子源发出一个质量为m、电荷量为q的正离子(初速度为零,重力不计),经加速电场加速后,从M点沿垂直于该点的场强方向进入静电分析器,在静电分析器中,离子沿半径为R的四分之一圆弧轨道做匀速圆周运动,并从N点射出静电分析器。而后离子由P点沿着既垂直于磁分析器的左边界,又垂直于磁场方向射入磁分析器中,最后离子沿垂直于磁分析器下边界的方向从Q点射出,并进入收集器。测量出Q点与圆心O2的距离为d。
(1)求静电分析器中离子运动轨迹处电场强度E的大小;
(2)求磁分析器中磁场的磁感应强度B的大小和方向;
(3)通过分析和必要的数学推导,请你说明如果离子的质量为0.9m,电荷量仍为q,其他条件不变,这个离子射出电场和射出磁场的位置是否变化。
如图所示,摩托车运动员做特技表演时,以v0=9.0m/s的初速度冲向高台,然后从高台水平飞出。若摩托车冲向高台的过程中牵引力的平均功率P=4.0kW,冲到高台顶端所用时间t=3.0s,人和车的总质量m=1.5×102kg,高台顶端距地面的高度h=7.2m,摩托车落地点到高台顶端的水平距离x=10.8m。不计空气阻力,取g=10m/s2。求:
(1)摩托车从高台顶端飞出到落地所用时间;
(2)摩托车落地时速度的大小;
(3)摩托车冲上高台的过程中克服摩擦阻力所做的功。
如图1所示,两根足够长的直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上,两导轨间距为L0、M、P两点间接有阻值为R的电阻。一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直。整套装置处于磁感应强度为B的匀强磁场中,磁场方向垂直斜面向下,导轨和金属杆的电阻可忽略。让ab杆沿导轨由静止开始下滑,导轨和金属杆接触良好,不计它们 之间的摩擦。
之间的摩擦。
(1)由b向a方向看到的装置如图2所示,请在此图中画出ab杆下滑过程中某时刻的受力示意图;
(2)在加速下滑过程中,当ab杆的速度大小为v时,求此时ab杆中的电流及其加速度的大小;
(3)求在下滑过程中,ab杆可以达到的速度最大值。