(本小题满分16分)
已知函数f(x)= 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
(Ⅰ)求f(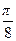 )的值;
)的值;
(Ⅱ)将函数y=f(x)的图象向右平移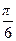 个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
(本小题满分12分)
已知函数f(x)=2sinxcosx+cos2x.
(1)求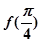 的值;
的值;
(2)求函数f(x)的最大值及取得最大值时x的值。
(本小题满分10分)
已知命题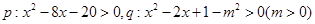 ,若
,若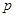 是
是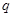 的充分不必要条件,求实数
的充分不必要条件,求实数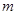 的取值范围.
的取值范围.
(本小题满分14分)
已知函数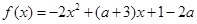 ,
,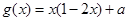 ,其中
,其中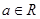 .
.
(1)若函数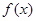 是偶函数,求函数
是偶函数,求函数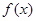 在区间
在区间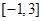 上的最小值;
上的最小值;
(2)用函数的单调性的定义证明:当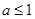 时,
时,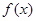 在区间
在区间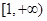 上为减函数;
上为减函数;
(3)当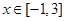 ,函数
,函数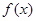 的图象恒在函数
的图象恒在函数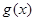 图象上方,求实数
图象上方,求实数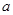 的取值范围.
的取值范围.
(本小题满分14分)
已知四棱锥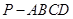 的底面
的底面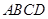 为平行四边形,
为平行四边形,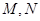 分别是棱
分别是棱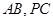 的中点,平面
的中点,平面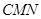 与平面
与平面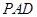 交于
交于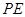 ,求证:
,求证: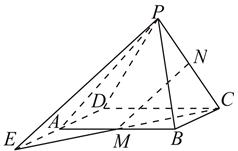
(1)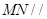 平面
平面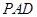 ;
;
(2)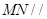
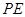 .
.
(本小题满分14分)
某市一家庭今年一月份、二月份和三月份煤气用量和支付费用如下表所示:
| 月份 |
用气量(立方米) |
煤气费(元) |
| 1 |
4 |
4.00 |
| 2 |
25 |
14.00 |
| 3 |
35 |
19.00 |
该市煤气收费的方法是:煤气费=基本费十超额费十保险费.
若每月用气量不超过最低额度 立方米时,只付基本费
立方米时,只付基本费 元和每户每月定额保险费
元和每户每月定额保险费 元;若用气量超过
元;若用气量超过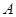 立方米时,超过部分每立方米付
立方米时,超过部分每立方米付 元.
元.
(1)根据上面的表格求 的值;
的值;
(2)记用户第四月份用气为 立方米,求他应交的煤气费
立方米,求他应交的煤气费 (元).
(元).