(本小题满分14分)
设二次函数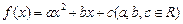 满足下列条件:
满足下列条件:
①当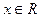 时,其最小值为0,且
时,其最小值为0,且 成立;
成立;
②当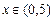 时,
时,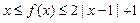 恒成立.
恒成立.
(1)求 的值;
的值;
(2)求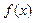 的解析式;
的解析式;
(3)求最大的实数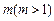 ,使得存在
,使得存在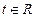 ,只要当
,只要当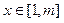 时,就有
时,就有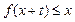 成立
成立
已知 ,
,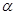 为第三象限角.
为第三象限角.
(1)求 的值;(2)求
的值;(2)求 的值.
的值.
已知数列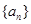 与
与 满足:
满足: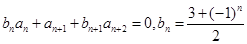 ,
, ,且
,且 .
.
(Ⅰ)求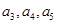 的值;
的值;
(Ⅱ)设 ,证明:
,证明: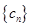 是等比数列
是等比数列
在数1和100之间插入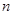 个实数,使得这
个实数,使得这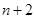 个数构成递增的等比数列,将这
个数构成递增的等比数列,将这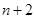 个数的乘积记作
个数的乘积记作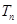 ,再令
,再令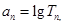
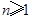 .
.
(Ⅰ)求数列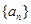 的通项公式;
的通项公式;
(Ⅱ)设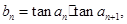 求数列
求数列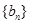 的前
的前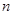 项和
项和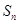 .
.
设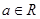 ,
,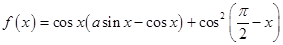 满足
满足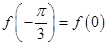 ,求函数
,求函数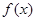 在
在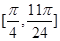 上的最大值和最小值.
上的最大值和最小值.
某房建公司在市中心用100万元购买一块土地,计划建造一幢每层为1000平方米的n
层楼房,第一层每平方米所需建筑费用(不包括购买土地费用)为600元,第二层每平
方米所需建筑费用为700元,…,以后每升高一层,每平方米的建筑费用增加100元.
(1)写出每平方米平均造价y(以百元为单位)用n表示的表达式;
(2)为使整个大楼每平方米的平均造价不超过1150元,则这幢大楼最多能造几层?