(本小题满分12分)
在高三年级某班组织的欢庆元旦活动中，有一项游戏规则如下：参与者最多有5次抽题并答题的机会.如果累计答对2道题，立即结束游戏，并获得纪念品；如果5次机会用完仍未累计答对2道题，也结束游戏，并不能获得纪念品.已知某参与者答对每道题答对的概率都是，且每道题答对与否互不影响.
（1）求该参与者获得纪念品的概率；
（2）记该参与者游戏时答题的个数为
，求的分布列及期望
（本小题满分12分）设向量
，向量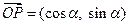
，
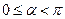．（1）若向量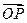
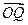，求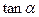
的值；（2）求
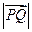的最大值及此时
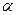的值．
（本小题16分）已知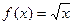
，g(x)=x+a (a>0)(1)当a=4时，求
的最小值；（2）当
时，不等式>1恒成立，求a的取值范围.
（本小题16分）已知数列
的前n项的和Sn，满足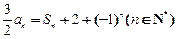
．
（1）求数列的通项公式．（2）设
，是否存在正整数k，使得当n≥3时，
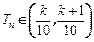如果存在，求出k；如果不存在，请说明理由．
（本小题满分15分）设
是公比大于1的等比数列，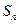
为数列的前
项和．已知
，且
构成等差数列．
（1）求数列的通项公式.（2）令
求数列
的前项和
．
（本小题15分）某工厂建造一间地面面积为12
的背面靠墙的矩形小房，房屋正面的造价为1200元/，房屋侧面的造价为800元/，屋顶的造价为5800元,如果墙高为3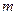
，且不计房屋背面的费用，则建造此小房的最低总造价是多少元？