(本小题满分13分)
已知正项数列{an}的首项a1=,函数f(x)=,g(x)=.
(1)若正项数列{an}满足an+1=f(an)(n∈N*),证明:{}是等差数列,并求数列{an}的通项公式;
(2)若正项数列{an}满足an+1≤f(an)(n∈N*),数列{bn}满足bn=,证明:b1+b2+…+bn<1;
(3)若正项数列{an}满足an+1=g(an),求证:|an+1-an|≤·()n-1
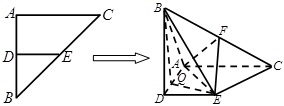
(本小题满分12分)在等腰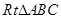 中,
中,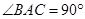 ,
,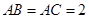 ,
,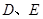 分别是边
分别是边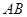 、
、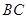 的中点,将
的中点,将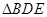 沿
沿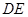 翻折,得到四棱锥
翻折,得到四棱锥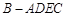 ,且
,且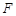 为棱
为棱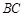 中点,
中点,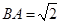 .
.
(1)求证: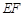
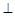 平面
平面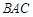 ;
;
(2)在线段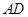 上是否存在一点
上是否存在一点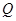 ,使得
,使得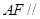 平面
平面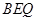 ?若存在,求二面角
?若存在,求二面角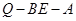 的余弦值,若不存在,请说明理由.
的余弦值,若不存在,请说明理由.
(本小题满分12分)现有4名学生参加演讲比赛,有A、B两个题目可供选择.组委会决定让选手通过掷一枚质地均匀的骰子选择演讲的题目,规则如下:选手掷出能被3整除的数则选择A题目,掷出其他的数则选择B题目.
(1)求这4个人中恰好有1个人选择B题目的概率;
(2)用X、Y分别表示这4个人中选择A、B题目的人数,记 ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望 .
.
(本小题满分12分)已知函数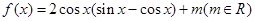 ,将
,将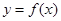 的图像向左平移
的图像向左平移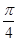 个单位后得到
个单位后得到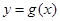 的图像,且
的图像,且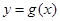 在区间
在区间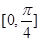 内的最大值为
内的最大值为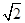 .
.
(1)求实数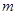 的值;
的值;
(2)在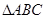 中,内角
中,内角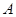 、
、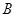 、
、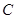 的对边分别是
的对边分别是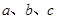 ,若
,若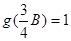 ,且
,且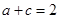 ,求
,求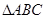 的周长
的周长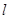 的取值范围.
的取值范围.
(本小题共13分)将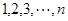 这
这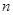 个数随机排成一列,得到的一列数
个数随机排成一列,得到的一列数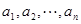 称为
称为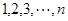 的一个排列.定义
的一个排列.定义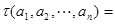
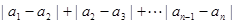 为排列
为排列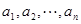 的波动强度.
的波动强度.
(Ⅰ)当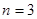 时,写出排列
时,写出排列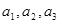 的所有可能情况及所对应的波动强度;
的所有可能情况及所对应的波动强度;
(Ⅱ)当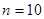 时,求
时,求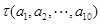 的最大值,并指出所对应的一个排列.
的最大值,并指出所对应的一个排列.
(本小题满分14分)已知椭圆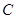 :
: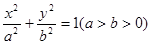 的上顶点为
的上顶点为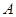 ,两个焦点为
,两个焦点为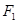 、
、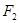 ,
,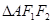 为正三角形且周长为6.
为正三角形且周长为6.
(Ⅰ)求椭圆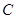 的标准方程;
的标准方程;
(Ⅱ)已知圆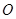 :
: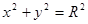 ,若直线
,若直线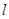 与椭圆
与椭圆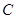 只有一个公共点
只有一个公共点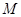 ,且直线
,且直线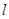 与圆
与圆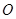 相切于点
相切于点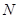 ;求
;求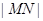 的最大值.
的最大值.