（满分16分）
记函数f(x)的定义域为D，若存在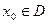
，使
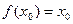成立，则称以
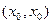为坐标的点为函数
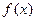图象上的不动点。
（1）若函数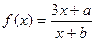
的图象上有两个关于原点对称的不动点，求
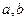应满足的条件；
（2）下述结论“若定义在Ｒ上的奇函数f(x)的图象上存在有限个不动点，则不动点有奇数个”是否正确？若正确，请给予证明，并举出一例；若不正确，请举出一反例说明
已知函数
．
（1）求函数
的最小正周期，最大值及取最大值时相应的
值；
（2）如果
，求的取值范围．
在正四棱锥
中，侧棱
的长为
，与
所成的角的大小等于
．
（1）求正四棱锥的体积；
（2）若正四棱锥的五个顶点都在球
的表面上，求此球的半径．
设函数
定义域为
，且
.
设点
是函数图像上的任意一点，过点分别作直线
和
轴的垂线，垂足分别为
．
（1）写出
的单调递减区间（不必证明）；
（2）设点的横坐标
，求
点的坐标（用的代数式表示）；
（3）设
为坐标原点，求四边形
面积的最小值.
等比数列
满足
，
，数列
满足
（1）求的通项公式；
（2）数列
满足
，
为数列的前
项和．求
；
（3）是否存在正整数
，使得
成等比数列？若存在，求出所有
的值；若不存在，请说明理由．
某海域有
、
两个岛屿，岛在岛正东4海里处。经多年观察研究发现，某种鱼群洄游的路线是曲线
，曾有渔船在距岛、岛距离和为8海里处发现过鱼群。以、所在直线为
轴，
的垂直平分线为
轴建立平面直角坐标系。
（1）求曲线的标准方程；
（2）某日，研究人员在、两岛同时用声纳探测仪发出不同频率的探测信号（传播速度相同），、两岛收到鱼群在
处反射信号的时间比为
，问你能否确定处的位置（即点的坐标）？