某海域有 、
、 两个岛屿,
两个岛屿, 岛在
岛在 岛正东4海里处。经多年观察研究发现,某种鱼群洄游的路线是曲线
岛正东4海里处。经多年观察研究发现,某种鱼群洄游的路线是曲线 ,曾有渔船在距
,曾有渔船在距 岛、
岛、 岛距离和为8海里处发现过鱼群。以
岛距离和为8海里处发现过鱼群。以 、
、 所在直线为
所在直线为 轴,
轴, 的垂直平分线为
的垂直平分线为 轴建立平面直角坐标系。
轴建立平面直角坐标系。
(1)求曲线 的标准方程;
的标准方程;
(2)某日,研究人员在 、
、 两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),
两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同), 、
、 两岛收到鱼群在
两岛收到鱼群在 处反射信号的时间比为
处反射信号的时间比为 ,问你能否确定
,问你能否确定 处的位置(即点
处的位置(即点 的坐标)?
的坐标)?
已知定义在R上的函数f(x) 同时满足:①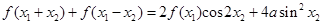 (
( R,a为常数);②
R,a为常数);②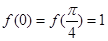 ;③当
;③当 时,
时, ≤2。
≤2。
求:(Ⅰ)函数 的解析式;(Ⅱ)常数a的取值范围。
的解析式;(Ⅱ)常数a的取值范围。
设函数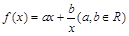 ,若
,若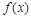 在点
在点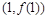 处的切线斜率为
处的切线斜率为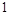 .
.
(Ⅰ)用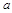 表示
表示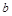 ;
;
(Ⅱ)设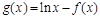 ,若
,若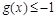 对定义域内的
对定义域内的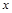 恒成立,
恒成立,
(ⅰ)求实数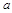 的取值范围;
的取值范围;
(ⅱ)对任意的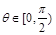 ,证明:
,证明: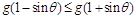 .
.
设点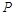 为圆
为圆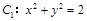 上的动点,过点
上的动点,过点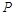 作
作 轴的垂线,垂足为
轴的垂线,垂足为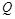 .动点
.动点 满足
满足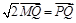 (其中
(其中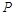 ,
,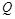 不重合).
不重合).
(Ⅰ)求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过直线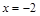 上的动点
上的动点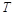 作圆
作圆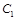 的两条切线,设切点分别为
的两条切线,设切点分别为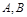 .若直线
.若直线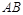 与(Ⅰ)中的曲线
与(Ⅰ)中的曲线 交于
交于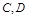 两点,求
两点,求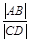 的取值范围.
的取值范围.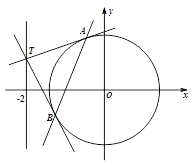
如图,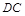 垂直平面
垂直平面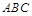 ,
,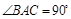 ,
,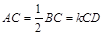 ,点
,点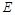 在
在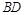 上,且
上,且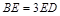 .
.
(Ⅰ)求证: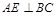 ;
;
(Ⅱ)若二面角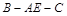 的大小为
的大小为 ,求
,求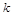 的值.
的值.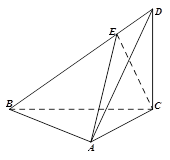
设公比为正数的等比数列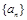 的前
的前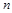 项和为
项和为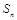 ,已知
,已知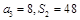 ,数列
,数列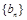 满足
满足 .
.
(Ⅰ)求数列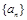 和
和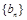 的通项公式;
的通项公式;
(Ⅱ)是否存在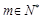 ,使得
,使得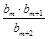 是数列
是数列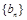 中的项?若存在,求出
中的项?若存在,求出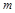 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.