设点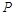 为圆
为圆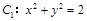 上的动点,过点
上的动点,过点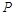 作
作 轴的垂线,垂足为
轴的垂线,垂足为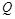 .动点
.动点 满足
满足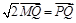 (其中
(其中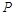 ,
,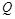 不重合).
不重合).
(Ⅰ)求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过直线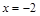 上的动点
上的动点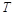 作圆
作圆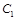 的两条切线,设切点分别为
的两条切线,设切点分别为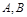 .若直线
.若直线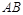 与(Ⅰ)中的曲线
与(Ⅰ)中的曲线 交于
交于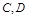 两点,求
两点,求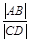 的取值范围.
的取值范围.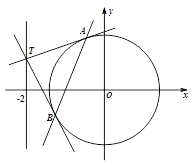
为了了解中学生的身高情况,对某校中学生同年龄的若干名女生的身高进行了测量,将所得数据整理后,画出频率分布直方图(如图),已知图中从左到右五个小组的频率分别为0.017,0.050,0.100,0.133,0.300,第三小组的频数为6(单位:cm).
某投资商准备在某市投资甲、乙、丙三个不同的项目,这三个项目投资是否成功相互独立,预测结果如表:
| 预测结果 项目 |
概率 |
|
| 成功 |
失败 |
|
| 甲 |
||
| 乙 |
||
| 丙 |
(1)求恰有一个项目投资成功的概率;
(2)求至少有一个项目投资成功的概率
集合M={a,b,c},N={-1,0,1},映射f:M→N满足f(a)+f(b)+f(c)=0,那么映射f:M→N的个数是多少?
已知f满足f(ab)=f(a)+f(b),且f(2)=p,f(3)=q,求f(72)的值.
已知二次函数f(x)=ax2+bx+c,(a<0)不等式f(x)>-2x的解集为(1,3).
(1)若方程f(x)+6a=0有两个相等的实根,求f(x)的解析式;
(2)若f(x)的最大值为正数,求实数a的取值范围.