已知双曲线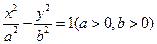
，顺次连接其实轴、虚轴端点所得四边形的面积为8，
（1）求双曲线焦距的最小值，并求出焦距最小时的双曲线方程；
（2）设A、B是双曲线上关于中心对称的两点，P是双曲线上另外一点，若直线PA、PB的斜率乘积等于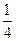
，求双曲线方程。
已知二次函数f（x）的最小值为1，且f（0）＝f（2）＝3．
（1）求f（x）的解析式；
（2）若f（x）在区间[2a，a＋1]上不单调，求a的取值范围
已知函数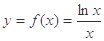
。
（Ⅰ）求函数
的图像在
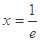处的切线方程；
（Ⅱ）求的最大值；
已知函数f（x）＝cos x（sin x＋cos x）－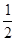
．
（1）若0＜α＜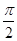
，且sin α＝
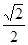，求f（α）的值；
（2）求函数f（x）的最小正周期及单调递增区间．
命题p：关于x的不等式x2＋（a－1）x＋a2≤0的解集为∅，命题q：函数y＝（2a2－a）x为增函数．若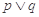
为真，
为假,求a的取值范围。
（本小题满分10分，不等式选讲）已知函数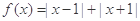
．
（1）求不等式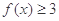
的解集；
（2）若关于
的不等式
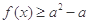在
上恒成立，求实数
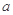的取值范围