对于给定首项 ,由递推公式 得到数列 ,对于任意的 ,都有 ,用数列 可以计算 .
(1)取
,计算
的值(精确到0.01);归纳出
的大小关系;
(2)当
时,证明:
.
(3)当 时,用数列 计算 的近似值,要求 ,请你估计 ,并说明理由
中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量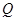 (简称血酒含量,单位是毫克/
(简称血酒含量,单位是毫克/ 毫升),当
毫升),当 时,为“酒后驾车”;当
时,为“酒后驾车”;当 时,为“醉酒驾车”.某市公安局交通管理部门于
时,为“醉酒驾车”.某市公安局交通管理部门于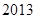 年
年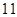 月的某天晚上
月的某天晚上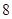 点至
点至 点在该市区解放路某处设点进行一次拦查行动,共依法查出了
点在该市区解放路某处设点进行一次拦查行动,共依法查出了 名饮酒后违法驾驶机动车者,如图为这
名饮酒后违法驾驶机动车者,如图为这 名驾驶员抽血检测后所得结果画出的频率分布直方图(其中
名驾驶员抽血检测后所得结果画出的频率分布直方图(其中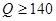 的人数计入
的人数计入 人数之内).
人数之内).
(Ⅰ)求此次拦查中“醉酒驾车”的人数;
(Ⅱ)从违法驾车的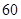 人中按“酒后驾车”和“醉酒驾车”利用分层抽样抽取
人中按“酒后驾车”和“醉酒驾车”利用分层抽样抽取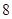 人做样本进行研究,再从抽取的
人做样本进行研究,再从抽取的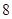 人中任取
人中任取 人,求
人,求 人中其中
人中其中 人为“酒后驾车”另
人为“酒后驾车”另 人为“醉酒驾车”的概率.
人为“醉酒驾车”的概率.
已知函数 的最大值为
的最大值为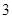 ,其图像相邻两条对称轴之间的距离为
,其图像相邻两条对称轴之间的距离为 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)设 ,求
,求 的值.
的值.
已知 ,
,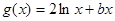 ,且直线
,且直线 与曲线
与曲线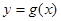 相切.
相切.
(1)若对 内的一切实数
内的一切实数 ,不等式
,不等式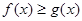 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)(ⅰ)当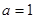 时,求最大的正整数
时,求最大的正整数 ,使得任意
,使得任意 个实数
个实数

 (
( 是自然对数的底数)都有
是自然对数的底数)都有 成立;
成立;
(ⅱ)求证:
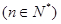 .
.
(1)已知定点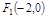 、
、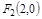 ,动点N满足
,动点N满足 (O为坐标原点),
(O为坐标原点), ,
, ,
,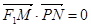 ,求点P的轨迹方程.
,求点P的轨迹方程.
(2)如图,已知椭圆 的上、下顶点分别为
的上、下顶点分别为 ,点
,点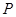 在椭圆上,且异于点
在椭圆上,且异于点 ,直线
,直线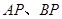 与直线
与直线 分别交于点
分别交于点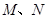 ,
,
(ⅰ)设直线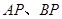 的斜率分别为
的斜率分别为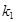 、
、 ,求证:
,求证: 为定值;
为定值;
(ⅱ)当点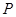 运动时,以
运动时,以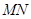 为直径的圆是否经过定点?请证明你的结论.
为直径的圆是否经过定点?请证明你的结论.
如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线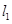 排水管,在路南侧沿直线
排水管,在路南侧沿直线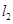 排水管(假设水管与公路的南,北侧在一条直线上且水管的大小看作为一条直线),现要在矩形区域ABCD内沿直线EF将
排水管(假设水管与公路的南,北侧在一条直线上且水管的大小看作为一条直线),现要在矩形区域ABCD内沿直线EF将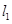 与
与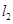 接通.已知AB = 60m,BC = 60
接通.已知AB = 60m,BC = 60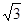 m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成角为
m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成角为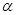 .矩形区域内的排管费用为W.
.矩形区域内的排管费用为W.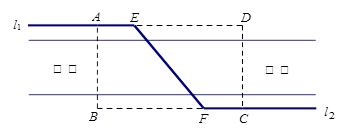
(1)求W关于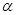 的函数关系式;
的函数关系式;
(2)求W的最小值及相应的角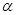 .
.