一质量为M =" 0.8" kg的中空的、粗细均匀的、足够长的绝缘细管，其内表面粗糙、外表面光滑；有一质量为m =" 0.2" kg、电荷量为q =" 0.1" C的带正电小滑块以水平向右的速度进入管内，如图甲。细管置于光滑的水平地面上，细管的空间能让滑块顺利地滑进去，示意图如图乙。运动过程中滑块的电荷量保持不变。空间中存在垂直纸面向里的水平匀强磁场，磁感强度为B =" 1.0" T。（取水平向右为正方向，g =" 10" m/s2）
(1)滑块以v0 = 10 m/s的初速度进入管内，则系统最终产生的内能为多少?
(2)滑块最终的稳定速度vt取决于滑块进入细管时的初速度v0，请以滑块的初速度v0为横坐标、滑块最终稳定时的速度vt 为纵坐标，在丙图中画出滑块的vt—v0图象（只需画出v0的取值范围在0至60 m/s的图象）。
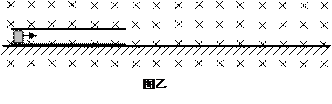
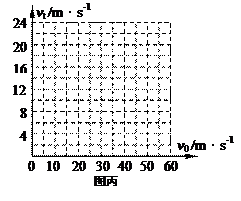
如图是甲、乙两物体同时、同地、同方向做直线运动的v-t图象.求甲、乙相遇时距出发点的距离是多少？甲、乙相遇前相距的最远距离是多少？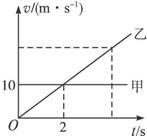
.一摩托车用30 m/s速度追赶在它前面100 m处的一辆汽车，若追了300 m才追上，求汽车的速度多大？
要求摩托车由静止开始在尽量短的时间内走完一段直道，然后驶入一段半圆形的弯道，但在弯道上行驶时车速不能太快，以免因离心作用而偏出车道．求摩托车在直道上行驶所用的最短时间.有关数据见表格．
| 启动加速度a1 |
4 m/s2 |
| 制动加速度a2 |
8 m/s2 |
| 直道最大速度v1 |
40 m/s |
| 弯道最大速度v2 |
20 m/s |
| 直道长度s |
218 m |
某同学是这样解的：要使摩托车所用时间最短，应先由静止加速到最大速度v1＝40 m/s，然后再减速到v2＝20 m/s，t1=
=…;t2=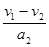
=…;t=t1+t2,你认为这位同学的解法是否合理？若合理，请完成计算；若不合理，请说明理由，并用你自己的方法算出正确结果．
一物体做匀变速直线运动，某时刻速度的大小为4 m/s，1 s后速度大小为10 m/s,在这1 s内该物体的（）
| A．位移大小可能小于4 m | B．位移大小可能大于10 m |
| C．加速度的大小可能小于4 m/s2 | D．加速度的大小可能大于10 m/s2 |
汽车由车站出发做直线运动，头5 s做匀加速直线运动，中间匀速行驶，最后10 s匀减速进站停车，已知全程共450 m，全程的平均速度为15 m/s，求：
（1）汽车最大速度；
（2）前4 s内的位移；
（3）最后3 s内的位移.