(本小题满分12分)在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB= ,EF∥AB,FG∥BC,EG∥AC. AB="2EF." 若M是线段AD的中点。求证:GM∥平面ABFE
,EF∥AB,FG∥BC,EG∥AC. AB="2EF." 若M是线段AD的中点。求证:GM∥平面ABFE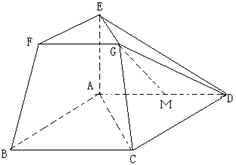
(本小题满分10分)选修4-5:不等式选讲
设函数 .
.
(Ⅰ)若 解不等式
解不等式 ;
;
(Ⅱ)如果关于 的不等式
的不等式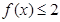 有解,求
有解,求 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
已知直线的极坐标方程为 ,圆
,圆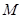 的参数方程为
的参数方程为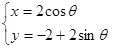 (其中
(其中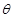 为参数).
为参数).
(Ⅰ)将直线的极坐标方程化为直角坐标方程;
(Ⅱ)求圆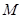 上的点到直线的距离的最小值.
上的点到直线的距离的最小值.
(本小题满分10分)如图,在 中,
中, ,
,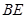 平分
平分 交
交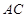 于点
于点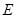 ,点
,点 在
在 上,
上,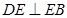 .
.
(1)求证: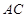 是△
是△ 的外接圆的切线;
的外接圆的切线;
(2)若 ,求
,求 的长.
的长.
(本小题满分12分)
已知函数 .(
.(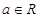 ).
).
(1)当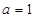 时,求函数
时,求函数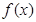 的极值;
的极值;
(2)若对 ,有
,有 成立,求实数
成立,求实数 的取值范围.
的取值范围.