（本小题满分10分）选修4-4：坐标系与参数方程
已知直线的极坐标方程为
，圆
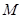的参数方程为
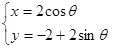（其中
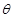为参数）.
（Ⅰ）将直线的极坐标方程化为直角坐标方程；
（Ⅱ）求圆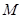上的点到直线的距离的最小值.
有三个新兴城镇，分别位于A、B、C三个点处，且AB=AC=13千米，BC＝10千米。今计划合建一个中心医院。为同时方便三个城镇，需要将医院建在BC的垂直平分线上的点P处。若希望点P到三个城镇距离的平方和最小，点P应该位于何处？
经过长期观测得到：在交通繁忙的时段内某公路汽车的车流量y（千辆／时）与汽车的平均速度v（千米／时）之间的函数关系为
在该时段内，当汽车的平均速度v为多少时，车流量最大？最大车流量是多少（精确到0.1千辆／时）？
若要求在该时段内车流量超过10千辆／时，则汽车的平均速度应该在什么范围内？
已知26辆货车以相同速度v由A地驶向400千米处的B地，每两辆货车间距离为d千米，现已知d与v的平方成正比，且当v=20（千米／时）时，d=1（千米）．
（1）写出d与v的函数关系；
（2）若不计货车的长度，则26辆货车都到达B地最少需要多少小时？此时货车速度是多少？
制定投资计划时，不仅要考虑可能获得的赢利，而且要考虑可能出现的亏损。某投资人打算投资甲、乙两个项目，根据预测，甲、乙项目可能的最大赢利率分别为100％和50％，可能的最大亏损率分别为30％和10％，投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元，问投资人对甲、乙两个项目各投资多少万元，才能使可能的赢利最大？
某电视机厂计划在下一个生产周期内生产两种型号的电视机，每台A型、B型电视机所得的利润分别为6和4个单位，而生产一台A型、B型电视机所耗原料分别为2和3个单位；所需工时分别为4和2个单位。如果允许使用的原料为100个单位，工时为120个单位，且A、B型电视机的产量分别不低于5台和10台，那么生产两种类型电视机各多少台，才能使利润最大？