(本小题满分12分)
已知两直线 .试确定
.试确定
 的值,使
的值,使
(1) //
//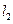 ;
;
(2)

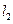 ,且
,且 在
在 轴上的
轴上的 截距为
截距为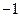 .
.
两个等差数列5,8,11,…和3,7,11,…都有100项,问它们有多少个共同的项?
梯子的最高一级宽33 cm,最低一级宽110 cm,中间还有10级,各级宽度成等差数列,计算中间各级的宽度.
已知函数f(x)= (a、b为常数,a≠0)满足f(2)=1,且f(x)=x有唯一解。如记xn=f(xn-1),且x1=1,n∈N*,求xn.
(a、b为常数,a≠0)满足f(2)=1,且f(x)=x有唯一解。如记xn=f(xn-1),且x1=1,n∈N*,求xn.
成等差数列的四个数之和为26,第二个数与第三个数之积为40,求这四个数.
从某校高一年级的1 002名新生中用系统抽样的方法抽取一个容量为100的身高样本,数据如下:(单位:cm)
| 168 |
165 |
171 |
167 |
170 |
165 |
170 |
152 |
175 |
174 |
| 165 |
170 |
168 |
169 |
171 |
166 |
164 |
155 |
164 |
158 |
| 170 |
155 |
166 |
158 |
155 |
160 |
160 |
164 |
156 |
162 |
| 160 |
170 |
168 |
164 |
174 |
171 |
165 |
179 |
163 |
172 |
| 180 |
174 |
173 |
159 |
163 |
172 |
167 |
160 |
164 |
169 |
| 151 |
168 |
159 |
168 |
176 |
155 |
165 |
165 |
169 |
162 |
| 177 |
158 |
175 |
165 |
169 |
151 |
163 |
166 |
163 |
167 |
| 178 |
165 |
158 |
170 |
169 |
159 |
155 |
163 |
153 |
155 |
| 167 |
163 |
164 |
158 |
168 |
167 |
161 |
162 |
167 |
158 |
| 161 |
165 |
174 |
156 |
167 |
166 |
162 |
161 |
164 |
166 |
(1)试作出该样本的频率分布表;
(2)画出频率分布直方图;
(3)估计总体中
身高小于160 cm的频率.