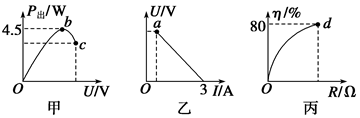
MN是一段半径为1m的光滑的1/4圆弧轨道,轨道上存在水平向右的匀强电场。轨道的右侧有一垂直纸面向内的匀强磁场,磁感应强度为B1=0.1T。现有一带电量为+1C质量为100g的带电小球从M点由静止开始自由下滑,恰能沿NP方向做直线运动,并进入右侧的复合场。(NP沿复合场的中心线)已知AB板间的电压为U=2V,板间距离d=2m,板的长度L=3m,若小球恰能从板的边沿飞出,NP沿复合场的中心线试求:
(1)小球运动到N点时的速度v;
(2)水平向右的匀强电场电场强度E;
(3)复合场中的匀强磁场的磁感应强度B2。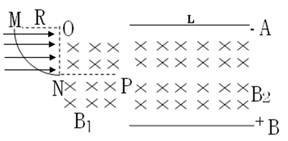
如图所示,在光滑的水平地面上,静止着质量为M =2.0kg的小车A,小车的上表面距离地面的高度为0.8m,小车A的左端叠放着一个质量为m=1.0kg的小物块B(可视为质点)处于静止状态,小物块与小车上表面之间的动摩擦因数μ=0.20。在小车A的左端正上方,用长为R=1.6m的不可伸长的轻绳将质量为m =1.0kg的小球C悬于固定点O点。现将小球C拉至使轻绳拉直且与竖起方向成θ=60°角的位置由静止释放,到达O点的正下方时,小球C与B发生弹性正碰(碰撞中无机械能损失),小物块从小车右端离开时车的速度为1m/s,空气阻力不计,取g=10m/s2. 求: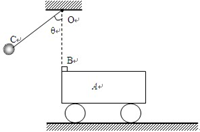
(1)小车上表面的长度L是多少?
(2)小物块落地时距小车右端的水平距离是多少?
两根完全相同的轻质弹簧将长度L=50cm,质量m=20g的金属杆悬挂起来,如图所示.金属杆处于水平状态,且处在垂直纸面向里的匀强磁场中,磁感应强度B=0.8T.(1)为了使弹簧处于原长,金属杆中应通以什么方向的电流?电流多大?(2)若金属杆中电流与(1)中求得数值相同,但方向相反,则两弹簧伸长多少? 已知每个弹簧的劲度系数均为k=0.1N/cm,g取10m/s2.
如图所示,固定在竖直平面内倾角为 的直轨道AB,与倾角可调的足够长的直轨道BC顺滑连接。现将一质量
的直轨道AB,与倾角可调的足够长的直轨道BC顺滑连接。现将一质量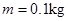 的小物块,从高为
的小物块,从高为 处静止释放,沿轨道AB滑下,并滑上倾角也为
处静止释放,沿轨道AB滑下,并滑上倾角也为 的轨道BC,所能达到的最大高度是
的轨道BC,所能达到的最大高度是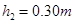 。若物块与两轨道间的动摩擦因数相同,不计空气阻力及连接处的能量损失。已知
。若物块与两轨道间的动摩擦因数相同,不计空气阻力及连接处的能量损失。已知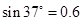 ,
,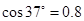 ,取g=10m/s2,求:
,取g=10m/s2,求: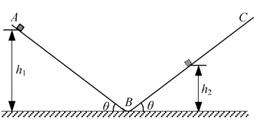
(1) 物块从释放到第一次速度为零的过程中,重力所做的功;
(2) 物块与轨道间的动摩擦因数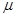 。
。
电动机的额定输出功率为10kW,问:
(1)它1min内可以做功多少功?
(2)用这台电动机竖直向上提升质量为2.5×102kg的货物,上升的最大速度为多大?取g=10m/s2,空气阻力不计。
如图所示,电源由n个电动势均为1.5 V、且内阻相同的电池串联组成,合上开关S,变阻器的滑片C从A端滑至B端的过程中,电路中一些物理量的变化规律由图甲、乙、丙给出(甲图为输出功率与路端电压关系曲线;乙图为路端电压与总电流关系曲线;丙图为电源的效率与外电路电阻关系曲线),电表、导线对电路的影响不计,求:
(1)组成电源的串联电池的个数;
(2)滑动变阻器的总阻值;
(3)将甲、乙、丙三个图上的a、b、c、d各点的坐标补齐。