已知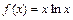
．
（1）求函数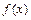
在区间
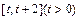上的最小值；
（2）对一切实数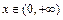
,
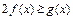恒成立，求实数
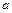的取值范围；
（3）证明对一切,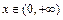
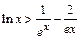恒成立．
（本小题满分14分）已知函数
,
且
.
（Ⅰ）求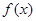
的定义域；（Ⅱ）判断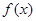的奇偶性并予以证明；
（Ⅲ）当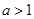
时，求使
的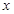
的取值范围.
（本小题满分14分）某公司试销一种成本单价为500元的新产品，规定试销时销售单价不低于成本单价，又不高于800元．经试销调查，发现销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y＝kx＋b(k≠0)，函数图象如图所示．
(1)根据图象，求一次函数y＝kx＋b(k≠0)的表达式；
(2)设公司获得的毛利润(毛利润＝销售总价－成本总价)为S元．试问销售单价定为多少时，该公司可获得最大毛利润？最大毛利润是多少？此时的销售量是多少？
(本小题满分13分)求下列函数的定义域和值域
（I）
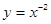；（II）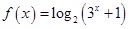
；（III）
．
（本小题满分12分）已知U=R,且A={x│-4<x<4},
,
求（I）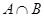
；（II）(CUA)∩B；（III）
.
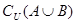在直角坐标系
中，圆C的参数方程为（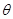
为参数
）
以O为极点，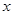
轴的非负半轴为极轴，并取相同的长度单位建立极坐标系，直线
的极坐标方程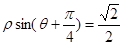
（1）求圆心的极坐标。
（2）若圆C上点到直线的最大距离为3，求
的值。