某农户以前在山上种了脐橙果树44株,前两年已有所收获。现进入第三年收获期。收获时,先随意采摘5株果树上的脐橙,称得每株果树上的脐橙质量如下(单位:千克):35,35,34,39,37
(1)根据样本平均数估计,这年脐橙的总产量约是多少?
(2)若市场上的脐橙售价为每千克5元,则这年该农户卖脐橙的收入将达多少元?
(3)已知该农户第一年卖脐橙的收入为5500元,根据以上估算,试求第二年、第三年卖脐橙收入的年平均增长率是多少?
如图,在△ABC中,AB=AC,D是BC中点,AE平分∠BAD交BC于点E,点O是AB上一点,⊙O过A、E两点,交AD于点G,交AB于点F.
(1)求证:BC与⊙O相切;
(2)当∠BAC=120°时,求∠EFG的度数.
随着人们经济收入的不断提高及汽车产业的快速发展,汽车已越来越多地进入普通家庭,成为居民消费新的增长点.据某市交通部门统计,2008年底全市汽车拥有量为15万辆,而截止到2010年底,全市的汽车拥有量已达21.6万辆.
(1)求2008年底至2010年底该市汽车拥有量的年平均增长率;
(2)为保护城市环境,缓解汽车拥堵状况,从2011年初起,该市交通部门拟控制汽车总量,要求到2012年底全市汽车拥有量不超过23.196万辆;另据估计,该市从2011年起每年报废的汽车数量是上年底汽车拥有量的10%.假定在这种情况下每年新增汽车数量相同,请你计算出该市每年新增汽车数多不能超过多少万辆.
如图,梯形ABCD中,AD∥BC,点M是BC的中点,且MA=MD.求证:四边形ABCD是等腰梯形.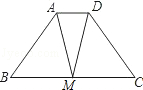
(1)计算: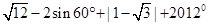
(2)解分式方程: .
.
已知,如图直线l的解析式为y=x+4,交x、y轴分别于A、B两点,点M(-1,3)在直线l上,O为原点.
(1)点N在x轴的负半轴上,且∠MNO=60°,则AN= ;
(2)点P在y轴上,线段PM绕点P旋转60°得到线段PQ,且点Q恰好在直线l上,则点P的坐标为 或 .