如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.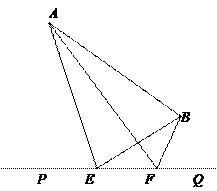
(1)判断 AB、AE的数量关系,并说明理由;
AB、AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果精确到0.1km).
(参考数据:≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49,
sin76°≈0.97,cos76°≈0.24)
如图,在矩形 中, , . 、 在对角线 上,且 , 、 分别是 、 的中点.
(1)求证: ;
(2)点 是对角线 上的点, ,求 的长.

如图,反比例函数 和一次函数 的图象相交于 , 两点.
(1)求一次函数的表达式;
(2)求出点 的坐标,并根据图象直接写出满足不等式 的 的取值范围.

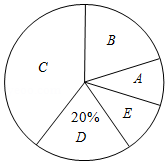
某校为了解七年级学生的体重情况,随机抽取了七年级 名学生进行调查,将抽取学生的体重情况绘制如下不完整的频数分布表和扇形统计图.
|
组别 |
体重(千克) |
人数 |
|
|
|
10 |
|
|
|
|
|
|
|
40 |
|
|
|
20 |
|
|
|
10 |
请根据图表信息回答下列问题:
(1)填空:
① ,
② ,
③在扇形统计图中, 组所在扇形的圆心角的度数等于 度;
(2)若把每组中各个体重值用这组数据的中间值代替(例如: 组数据中间值为40千克),则被调查学生的平均体重是多少千克?
(3)如果该校七年级有1000名学生,请估算七年级体重低于47.5千克的学生大约有多少人?
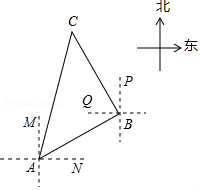
如图,一艘船由 港沿北偏东 方向航行 至 港,然后再沿北偏西 方向航行 至 港.
(1)求 , 两港之间的距离(结果保留到 ,参考数据: , ;
(2)确定 港在 港的什么方向.
某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同,求该工厂原来平均每天生产多少台机器?