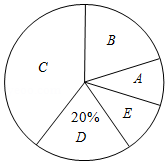
某校为了解七年级学生的体重情况，随机抽取了七年级 $m$名学生进行调查，将抽取学生的体重情况绘制如下不完整的频数分布表和扇形统计图．

组别	体重（千克）	人数
$A$	$37.5⩽x<42.5$	10
$B$	$42.5⩽x<47.5$	$n$
$C$	$47.5⩽x<52.5$	40
$D$	$52.5⩽x<57.5$	20
$E$	$57.5⩽x<62.5$	10

请根据图表信息回答下列问题：

（1）填空：

① $m=$　　，

② $n=$　　，

③在扇形统计图中， $C$组所在扇形的圆心角的度数等于　　度；

（2）若把每组中各个体重值用这组数据的中间值代替（例如： $A$组数据中间值为40千克），则被调查学生的平均体重是多少千克？

（3）如果该校七年级有1000名学生，请估算七年级体重低于47.5千克的学生大约有多少人？

科目 数学   题型 解答题   难度 中等

知识点： 用样本估计总体 频数（率）分布表 扇形统计图