(本小题共14分)已知函数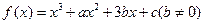 ,且
,且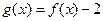 是奇函数.
是奇函数.
(Ⅰ)求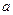 ,
,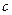 的值; (Ⅱ)求函数
的值; (Ⅱ)求函数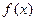 的单调区间.
的单调区间.
选修4-5:不等式选讲(本小题满分10分)
若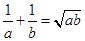 ,且
,且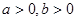 ,求
,求 的最小值.
的最小值.
选修4-4:坐标系与参数方程[(本小题满分10分)
己知直线  的参数方程为
的参数方程为 (t为参数),圆C的参数方程为
(t为参数),圆C的参数方程为 .(a>0.
.(a>0.  为参数),点P是圆C上的任意一点,若点P到直线
为参数),点P是圆C上的任意一点,若点P到直线 的距离的最大值为
的距离的最大值为 ,求a的值。
,求a的值。
.选修4-2:矩阵与变换(本小题满分10分)
已知 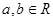 ,矩阵
,矩阵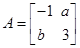 所对应的变换
所对应的变换 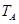 将直线
将直线 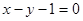 变换为自身,求a,b的值。
变换为自身,求a,b的值。
选修4-1:几何证明选讲
如图, 0是△ABC的外接圆,AB = AC,延长BC到点D,使得CD = AC,连结AD交
0是△ABC的外接圆,AB = AC,延长BC到点D,使得CD = AC,连结AD交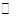 O于点E.求证:BE平分
O于点E.求证:BE平分 ABC
ABC
(本小题满分16分)己知函数
(1)若 ,求函数
,求函数  的单调递减区间;
的单调递减区间;
(2)若关于x的不等式  恒成立,求整数 a的最小值:
恒成立,求整数 a的最小值:
(3)若  ,正实数
,正实数  满足
满足  ,证明:
,证明: 