数列 的前n项和记为
的前n项和记为 ,前
,前 项和记为
项和记为
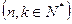 ,对给定的常数
,对给定的常数 ,若
,若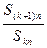 是与
是与 无关的非零常数
无关的非零常数 ,则称该数列
,则称该数列 是“
是“ 类和科比数列”,
类和科比数列”,
(理科做以下(1)(2)(3))
(1)、已知 ,求数列
,求数列 的通项公式;
的通项公式;
(2)、证明(1)的数列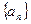 是一个 “
是一个 “ 类和科比数列”;
类和科比数列”;
(3)、设正数列 是一个等比数列,首项
是一个等比数列,首项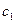 ,公比
,公比
 ,若数列
,若数列 是一个 “
是一个 “ 类和科比数列”,探究
类和科比数列”,探究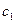 与
与 的关系
的关系
已知二次函数 ,且不等式
,且不等式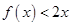 的解集为
的解集为 .
.
(1)方程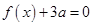 有两个相等的实根,求
有两个相等的实根,求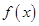 的解析式;
的解析式;
(2)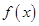 的最小值不大于
的最小值不大于 ,求实数
,求实数 的取值范围;
的取值范围;
(3) 如何取值时,函数
如何取值时,函数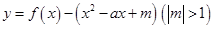 存在零点,并求出零点.
存在零点,并求出零点.
在平面直角坐标系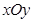 中,点
中,点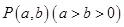 为动点,
为动点,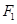 、
、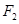 分别为椭圆
分别为椭圆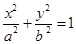 的左、右焦点.已知
的左、右焦点.已知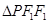 为等腰三角形.
为等腰三角形.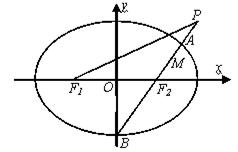
(1)求椭圆的离心率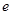 ;
;
(2)设直线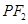 与椭圆相交于
与椭圆相交于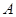 、
、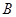 两点,
两点,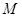 是直线
是直线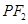 上的点,满足
上的点,满足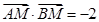 ,求点
,求点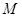 的轨迹
的轨迹
方程.
已知等差数列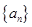 的公差
的公差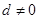 ,它的前
,它的前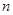 项和为
项和为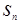 ,若
,若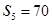 ,且
,且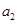 、
、 、
、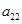 成等比数列.
成等比数列.
(1)求数列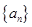 的通项公式;
的通项公式;
(2)设数列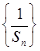 的前
的前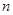 项和为
项和为 ,求证:
,求证: .
.
如图,已知三棱锥 的侧棱
的侧棱 、
、 、
、 两两垂直,且
两两垂直,且 ,
,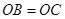
 ,
, 是
是 的中点.
的中点.
(1)求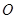 点到面
点到面 的距离;
的距离;
(2)求二面角 的正弦值.
的正弦值.
某社团组织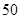 名志愿者利用周末和节假日参加社会公益活动,活动内容是:1.到各社区宣传慰问,倡导文明新风;2.到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示:
名志愿者利用周末和节假日参加社会公益活动,活动内容是:1.到各社区宣传慰问,倡导文明新风;2.到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示:
| 宣传慰问 |
义工 |
总计 |
|
 岁至 岁至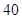 岁 岁 |
 |
 |
 |
大于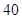 岁 岁 |
 |
 |
 |
| 总计 |
 |
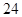 |
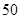 |
(1)分层抽样方法在做义工的志愿者中随机抽取 名,年龄大于
名,年龄大于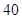 岁的应该抽取几名?
岁的应该抽取几名?
(2)上述抽取的 名志愿者中任取
名志愿者中任取 名,求选到的志愿者年龄大于
名,求选到的志愿者年龄大于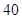 岁的人数的数学期望.
岁的人数的数学期望.