如图，四边形ABCD是菱形，点G是BC延长线上一点，连接AG，分别交BD、CD于点E、F，连接CE．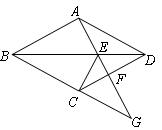
（1）求证：∠DAE＝∠DCE；
（2）当AE＝2EF时，判断FG与EF有何等量关系？并证明你的结论？
先化简
，再从0、1、2、3中选一个你喜欢的数代入求值。
解方程：
（1）
；
（2）
；
在ΔABC中，AB=AC
（1）如图1，如果∠BAD=30°，AD是BC上的高，AD=AE，则∠EDC=__________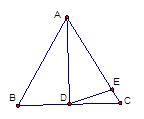
（2）如图2，如果∠BAD=40°，AD是BC上的高，AD=AE，则∠EDC=__________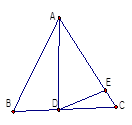
（3）思考：通过以上两题，你发现∠BAD与∠EDC之间有什么关系？
请用式子表示：____________________
（4）如图3，如果AD不是BC上的高，AD=AE，是否仍有上述关系？如有，请你写出来，并说明理由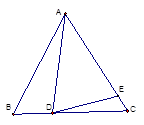
在直角坐标系中，长方形ABCD的边AB可表示为（-2，y）（-1≤y≤2），边AD可表示为（x，2）（-2≤x≤4）。求：
（1）长方形各顶点的坐标；
（2）长方形ABCD的周长.
（本题8分）某校为了奖励获奖的学生，买了若干本课外读物，如果每人送3本，还余8本；如果前面每人送5本，则最后一人得到的课外读物有但不足4本。设该校买了m本课外读物，有x名学生获奖，试解：
（1）用含x的代数式表示
；
（2）获奖人数至少有多少人？并求出此时所买课外读物的本数。