(本小题满分14分)
某商场以100元/件的价格购进一批衬衣,以高于进货价的价格出售,销售期有淡季与旺季之分,通过市场调查发现:
①销售量 (件)与衬衣标价
(件)与衬衣标价 (元/件)在销售旺季近似地符合函数关系:
(元/件)在销售旺季近似地符合函数关系: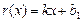 ,在销售淡季近似地符合函数关系:
,在销售淡季近似地符合函数关系: ,其中
,其中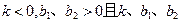 为常数;
为常数;
②在销售旺季,商场以140元/件的价格销售能获得最大销售利润;
③若称①中 时的标价
时的标价 为衬衣的“临界价格”,则销售旺季的“临界价格”是销售淡季的“临界价格”的1.5倍.
为衬衣的“临界价格”,则销售旺季的“临界价格”是销售淡季的“临界价格”的1.5倍.
请根据上述信息,完成下面问题:
(Ⅰ)填出表格中空格的内容:
 数量关系 数量关系销售关系 |
标价(元/件) |
销售量 (件)(含 (件)(含 、 、 或 或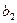 ) ) |
销售总利润 (元)与标价 (元)与标价 (元/件)的函数关系式 |
| 旺季 |
 |
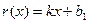 |
|
| 淡季 |
 |
|
|
(Ⅱ)在销售淡季,该商场要获得最大销售利润,衬衣的标价应定为多少元/件?
(本小题满分8分)
如图,已知点 是平行四边形
是平行四边形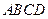 所在平面外的一点,
所在平面外的一点, ,
,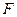 分别是
分别是 ,
, 上的点且
上的点且 ,求证:
,求证: 平面
平面 .
.
(本小题满分8分)
将圆心角为1200,面积为3 的扇形,作为圆锥的侧面,求圆锥的表面积和体积.
的扇形,作为圆锥的侧面,求圆锥的表面积和体积.
设 ,函数
,函数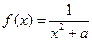 .
.
(Ⅰ)证明:存在唯一实数 ,使
,使 ;
;
(Ⅱ)定 义数列
义数列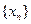 :
: ,
, ,
,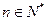 .
.
(i)求证:对任意正整数n都有 ;
;
(ii) 当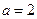 时,若
时,若 ,
,
证明:当k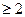 时,对任意
时,对任意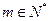 都有:
都有: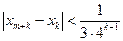
已知函数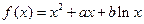 (
(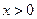 ,实数
,实数 ,
, 为常数).
为常数).
(Ⅰ)若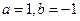 ,求函数
,求函数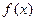 的极值;
的极值;
(Ⅱ)若 ,讨论函数
,讨论函数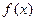 的单
的单 调性.
调性.
双曲线的中心为原点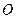 ,焦点在
,焦点在 轴上,两条渐近线分别为
轴上,两条渐近线分别为 ,经过右焦点
,经过右焦点
 垂直于
垂直于 的直线分别交
的直线分别交 于
于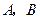 两点.已知
两点.已知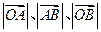 成等差数列,且
成等差数列,且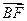 与
与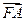 同向.
同向.
(Ⅰ)求双曲线的离心率;
(Ⅱ )设
)设 被双曲线所截
被双曲线所截 得的线段的长为4,求双曲线的方程.
得的线段的长为4,求双曲线的方程.