(本题满分5分)
先化简,再求值: ,其中
,其中 ,
,
在2010年上海世博会举行期间,某初级中学组织全校学 生参观世博园,亲身体验“城市让生活更美好”的世博理念.为了解学生就学校统一组织参观过的5个场馆的最喜爱程度,随机抽取该校部分学生进行问卷调查(每人应选且只能选一个场馆),数据整理后,绘制成如下的统计图:
生参观世博园,亲身体验“城市让生活更美好”的世博理念.为了解学生就学校统一组织参观过的5个场馆的最喜爱程度,随机抽取该校部分学生进行问卷调查(每人应选且只能选一个场馆),数据整理后,绘制成如下的统计图: 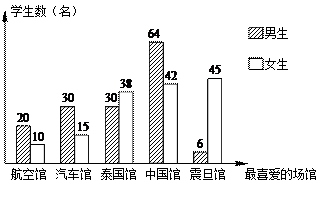
请根据统计 图提供的信息回答下列问题:
图提供的信息回答下列问题:
(1)本次随机抽样调查的样本容量是;
(2)本次随机抽样调查的统计数据中,男生最喜爱场馆的中位数是名;
(3)估计该校女生最喜爱泰国馆的约占全校学生数的%(保留三个有效数字);
(4)如果该校共有2000名学生,而且六、七、八年级学生人数总和比九年级学生人数的3倍还多200名,试通过计算估计该校九年级学生最喜爱中国馆的人数约为多少名?
如图,已知AB是⊙O的直径,CD⊥A
 B,垂足为点E,如果BE=OE,AB=10cm,求△ACD的周长.
B,垂足为点E,如果BE=OE,AB=10cm,求△ACD的周长.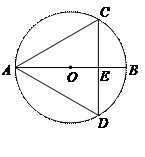
先化简,再求值: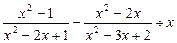 ,其中
,其中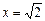 .
.
求不等式组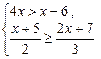 的整数解.
的整数解.
(本题共3小题,第(1)小题4分,第(2)、(3)小题每小题5分,满分14分)
如图,在矩形ABCD中,点E在边AD上,联结BE,∠ABE = 30°,BE = DE,联结BD.点M为线段DE上的任意一点,过点M作MN // BD,与BE相交于点N.
(1)如果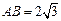 ,求边AD的长;
,求边AD的长;
(2)如图1,在(1)的条件下,如果点M为线段DE 的中点,联结CN.过点M作MF⊥CN,垂足为点F,求线段MF的长;
的中点,联结CN.过点M作MF⊥CN,垂足为点F,求线段MF的长;
(3)试判断BE、MN、MD这三条线段的长度之间有怎样的数量关系?请证明你的结论.
