如图所示,两块相同的金属板正对着水平放置,金属板长为L,两板间距离为d。上极板的电势比下极板高U。质量为m、带电量为q的正离子束,沿两板间中心轴线以初速度υ0进入两板间,最终都能从两板间射出。不计离子重力及离子间相互作用的影响。
(1)求离子在穿过两板的过程中沿垂直金属板方向上移动的距离y;
(2)若在两板间加垂直纸面的匀强磁场,发现离子束恰好沿直线穿过两板,求磁场磁感应强度B的大小和方向;
(3)若增大两板间匀强磁场的强度,发现离子束在穿过两板的过程中沿垂直金属板方向上移动的距离也为y,求离子穿出两板时速度的大小υ。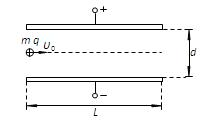
如图,可视为质点的三物块A、B、C放在倾角为30°的固定斜面上,物块与斜面间的动摩擦因数μ=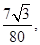 A与B紧靠一起,C紧靠在固定挡板上,三物块的质量分别为mA="0.80" kg、mB="0.64" kg、mC="0.50" kg,其中A不带电,B、C均带正电,且qC=2.0×10-5 C,开始时三个物块均能保持静止且与斜面间均无摩擦力作用,B、C间相距L="1.0" m.如果选定两点电荷在相距无穷远处的电势能为0,则相距为r时,两点电荷具有的电势能可表示为Ep=k
A与B紧靠一起,C紧靠在固定挡板上,三物块的质量分别为mA="0.80" kg、mB="0.64" kg、mC="0.50" kg,其中A不带电,B、C均带正电,且qC=2.0×10-5 C,开始时三个物块均能保持静止且与斜面间均无摩擦力作用,B、C间相距L="1.0" m.如果选定两点电荷在相距无穷远处的电势能为0,则相距为r时,两点电荷具有的电势能可表示为Ep=k 现给A施加一平行于斜面向上的力F,使A在斜面上做加速度a="1.5" m/s2的匀加速直线运动,假定斜面足够长.已知静电力常量k=9.0×109 N·m2/C2,取g="10" m/s2.求:
现给A施加一平行于斜面向上的力F,使A在斜面上做加速度a="1.5" m/s2的匀加速直线运动,假定斜面足够长.已知静电力常量k=9.0×109 N·m2/C2,取g="10" m/s2.求: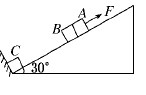
(1)B物块的带电荷量qB.
(2)A、B运动多长距离后开始分离.
(3)从开始施力到A、B分离,力F对A物块做的功.
如图所示,空间存在着电场强度E=2.5×102 N/C、方向竖直向上的匀强电场,在电场内一长为L="0." 5 m的绝缘细线一端固定于O点,另一端拴着质量m="0.5" kg、电荷量q=4×10-2 C的小球.现将细线拉至水平位置,将小球由静止释放,当小球运动到最高点时细线受到的拉力恰好达到它能承受的最大值而断裂.取g="10" m/s2.求:
(1)小球的电性;
(2)细线能承受的最大拉力值.
如图所示,光滑绝缘竖直细杆与以正电荷Q为圆心的圆周交于B,C两点.一质量为m,电荷量为-q的空心小球从杆上A点从静止开始下落.设AB=BC=h,小球滑到B点时速度为 求:
求:
(1)小球滑至C点的速度;
(2)A,C两点的电势差.
在光滑绝缘的水平面上,用长为2L的绝缘轻杆连接两个质量均为m的带电小球A和B.A球的带电荷量为+2q,b球的带电荷量为-3q,组成一带电系统,如图所示,虚线MP为AB两球连线的垂直平分线,虚线 NQ与MP平行且相距4L.最初A和B分别静止于虚线MP的两侧,距MP的距离均为L,且A球距虚线 NQ的距离为3L.若视小球为质点,不计轻杆的质量,在虚线MP、 NQ间加上水平向右的匀强电场E后,求:
(1) B球刚进入电场时,带电系统的速度大小.
(2)带电系统从开始运动到速度第一次为零所需时间以及B球电势能的变化量.
为使带负电的点电荷q在一匀强电场中沿直线匀速地由A运动到B,必须对该电荷施加一个恒力F,如图所示,若AB="0.4" m,α=37°,q=-3×10-7 C,F=1.5×10-4 N,A点的电势UA="100" V.(不计负电荷受到的重力)
(1)在图中用实线画出电场线,用虚线画出通过A、B两点的等势线,并标明它们的电势.
(2)求q在由A到B的过程中电势能的变化量是多少?