已知直角梯形OABC在如图所示的平面直角坐标系中,AB∥OC,AB=10,OC=22,BC=15,动点M从A点出发,以每秒一个单位长度的速度沿AB向点B运动,同时动点N从C点出发,以每秒2个单位长度的速度沿CO向O点运动.当其中一个动点运动到终点时,两个动点都停止运动.
(1)求B点坐标;
(2)设运动时间为t秒;
①当t为何值时,四边形OAMN的面积是梯形OABC面积的一半;
②当t为何值时,四边形OAMN的面积最小,并求出最小面积;
③若另有一动点P,在点M、N运动的同时,也从点A出发沿AO运动.在②的条件下,PM+PN的长度也刚好最小,求动点P的速度.
已知反比例函数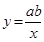 ,当
,当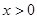 时,
时, 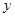 随
随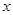 的增大而增大,则关
的增大而增大,则关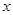 于的方程
于的方程 的解的情况是.
的解的情况是.
已知 ,那么
,那么 可化简为.
可化简为.
写出一个无理数,使它与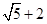 的积为有理数____ ____.
的积为有理数____ ____.
一开口向上的抛物线与x轴交于A(m-2,0),B(m+2,0)两点,记抛物线顶点为C,且AC⊥BC.
(1)若m为常数,求抛物线的解析式;
(2)若m为小于0的常数,那么(1)中的抛物线经过怎么样的平移可以使顶点在坐标原点?
(3)设抛物线交y轴正半轴于D点,问是否存在实数m,使得△BOD为等腰三角形?若存在,求出m的值;若不存在,请说明理由.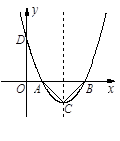
某公司经销某品牌运动鞋,年销售量为10万双,每双鞋按250元销售,可获利25﹪,设每双鞋的成本价为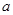 元.
元.
(1)试求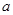 的值;
的值;
(2)为了扩大销售量,公司决定拿出一定量的资金做广告,根据市场调查,若每年投入广告费为 (万元)时,产品的年销售量将是原销售量的
(万元)时,产品的年销售量将是原销售量的 倍,且
倍,且 与
与 之间的关系如图所示,可近似看作是抛物线的一部分.
之间的关系如图所示,可近似看作是抛物线的一部分.
①根据图象提供的信息,求 与
与 之间的函数关系式;
之间的函数关系式;
②求年利润 (万元)与广告费
(万元)与广告费 (万元)之间的函数关系式,并请回答广告费
(万元)之间的函数关系式,并请回答广告费 (万元)在什么范围内,公司获得的年利润
(万元)在什么范围内,公司获得的年利润 (万元)随广告费的增大而增多?
(万元)随广告费的增大而增多?
(注:年利润 =年销售总额-成本费-广告费)
=年销售总额-成本费-广告费)