如图，在矩形ABCD中，BC=24cm，P，Q，M，N分别从A，B，C，D出发沿AD，BC，CB，DA方向在矩形的边上同时运动，当有一个点先到达所在运动边的另一个端点时，运动即停止．
已知在相同时间内，若BQ="x" cm(
)，则AP="2x" cm，CM="3x" cm，DN="x2" cm．
（1）当x为何值时，以P、N两点重合？
（2）问Q、M两点能重合吗？若Q、M两点能重合，则求出相应的x的值；若Q、M两点不能重合，请说明理由。
（3）当x 为何值时，以P，Q，M，N为顶点的四边形是平行四边形。
扇形的圆心角为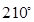
，弧长是
，求扇形的面积．
如图所示，正方形
是以金属丝围成的，其边长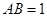
，把此正方形的金属丝重新围成扇形的
，使
，
不变，问正方形面积与扇形面积谁大？大多少？由计算得出结果．
如图正方形ABCD边长为1，G为CD边上的一个动点（点G与C、D不重合），以CG为一边向正方形ABCD外作正方形GCEF，连接DE交BG的延长线于点H。
（1）求证：BH⊥DE；
（2）当BH垂直平分DE时，求CG的长度？请说明理由。
某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，若每千克涨价为1元，日销售量将减少20千克，现该商场要保证每天盈利6000元，同时又要使顾客得到实惠，那么每千克应涨价多少元？
（6分)王阿姨绣了一幅长80㎝，宽50㎝的十字绣风景画，在裱画时，画的四周镶上宽度相等的金边，为了使整幅画的面积达到5400㎝2，问金边的宽度是多少？