函数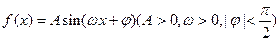 的部分图象如图所示。
的部分图象如图所示。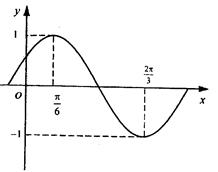
(I)求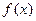 的最小正周期及解析式;
的最小正周期及解析式;
(II)设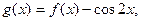 求函数
求函数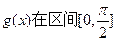 上的最大值和最小值
上的最大值和最小值
如图所示:用篱笆围成一个一边靠墙的矩形菜园 ,假设墙有足够长.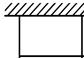
(Ⅰ) 若篱笆的总长为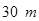 ,则这个矩形的长,宽各为多少时,菜园的面积最大?
,则这个矩形的长,宽各为多少时,菜园的面积最大?
(Ⅱ) 若菜园的面积为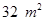 ,则这个矩形的长,宽各为多少时,篱笆的总长最短?
,则这个矩形的长,宽各为多少时,篱笆的总长最短?
已知函数 .
.
(Ⅰ) 求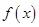 的最小值及相应
的最小值及相应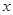 的值;
的值;
(Ⅱ) 解关于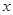 的不等式:
的不等式: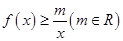 .
.
如图: 在 中,角
中,角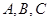 的对边分别为
的对边分别为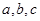

(Ⅰ) 若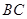 边上的中点为
边上的中点为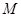 ,且
,且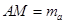 ,
,
求证: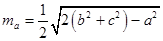 ;
;
(Ⅱ) 若 是锐角三角形,且
是锐角三角形,且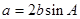 .
.
求 的取值范围.
的取值范围.
数列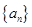 满足
满足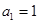 ,
, (
(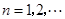 ),
),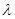 是常数.
是常数.
(Ⅰ)当 时,求
时,求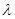 及
及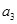 的值;
的值;
(Ⅱ)数列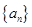 是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由.
是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由.
已知函数 是
是 上的增函数,
上的增函数,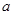 ,
,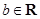 .
.
(Ⅰ)若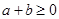 ,求证:
,求证: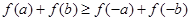 ;
;
(Ⅱ)判断(Ⅰ)中命题的逆命题是否成立,并证明你的结论.