如图所示:用篱笆围成一个一边靠墙的矩形菜园 ,假设墙有足够长.
(Ⅰ) 若篱笆的总长为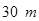 ,则这个矩形的长,宽各为多少时,菜园的面积最大?
,则这个矩形的长,宽各为多少时,菜园的面积最大?
(Ⅱ) 若菜园的面积为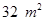 ,则这个矩形的长,宽各为多少时,篱笆的总长最短?
,则这个矩形的长,宽各为多少时,篱笆的总长最短?
已知关于x的不等式 (其中
(其中 ).
).
(1)当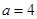 时,求不等式的解集;
时,求不等式的解集;
(2)若不等式有解,求实数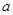 的取值范围
的取值范围
在平面直角坐标系中,曲线C1的参数方程为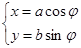 (a>b>0,
(a>b>0,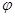 为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M
为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M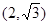 对应的参数
对应的参数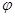 =
=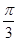 ,
, 与曲线C2交于点D
与曲线C2交于点D
(1)求曲线C1,C2的方程;
(2)A(ρ1,θ),Β(ρ2,θ+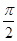 )是曲线C1上的两点,求
)是曲线C1上的两点,求 的值。
的值。
已知PQ与圆O相切于点A,直线PBC交圆于B、C两点,D是圆上一点,且AB∥CD,DC的延长线交PQ于点Q.
求证:
若AQ=2AP,AB= ,BP=2,求QD.
,BP=2,求QD.
已知函数 (
( )
)
(1)当a=2时,求 在区间[e,e2]上的最大值和最小值;
在区间[e,e2]上的最大值和最小值;
(2)如果函数 、
、 、
、 在公共定义域D上,满足
在公共定义域D上,满足 <
< <
< ,那么就称
,那么就称 为
为 、
、 的“伴随函数”.已知函数
的“伴随函数”.已知函数 ,
, ,若在区间(1,+∞)上,函数
,若在区间(1,+∞)上,函数 是
是 、
、 的“伴随函数”,求a的取值范围。
的“伴随函数”,求a的取值范围。
已知椭圆 :
: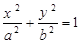 (
( )过点(2,0),且椭圆C的离心率为
)过点(2,0),且椭圆C的离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)若动点 在直线
在直线 上,过
上,过 作直线交椭圆
作直线交椭圆 于
于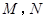 两点,且
两点,且 为线段
为线段 中点,再过
中点,再过 作直线
作直线 .求直线
.求直线 是否恒过定点,若果是则求出该定点的坐标,不是请说明理由。
是否恒过定点,若果是则求出该定点的坐标,不是请说明理由。