设A、B分别为椭圆 的左、右顶点,椭圆的长轴长为4,且点
的左、右顶点,椭圆的长轴长为4,且点 在该椭圆上。
在该椭圆上。
(I)求椭圆的方程;
(II)设P为直线x=4上不同于点(4,0)的任意一点,若直线AP与椭圆相交于A的点
M,证明: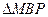 为锐角三角形
为锐角三角形
已知数列{an}满足a1=2,对于任意的n∈N,都有an>0,且(n+1)a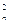 +anan+1-na
+anan+1-na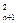 =0,又知数列{bn}:b1=2n-1+1
=0,又知数列{bn}:b1=2n-1+1
(1)求数列{an}的通项an以及它的前n项和Sn;
(2)求数列{bn}的前n项和Tn;
(3)猜想Sn和Tn的大小关系,并说明理由.
如图,平行六面体ABCD-A'B'C'D'中,AC=2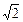 ,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
(1)求侧棱AA'与底面ABCD所成角的大小;
(2)求侧面A'ADD'底面ABCD所成二面角的正切值;
(3)求四棱锥C-A'ADD'的体积.
在三角形ABC中,三内角满足A+C=2B,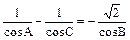 ,求cos
,求cos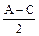 的值
的值
解关于x的不等式:loga(x2-x-2)>loga(x- )+1(a>0,a≠1)
)+1(a>0,a≠1)
已知:如图,射线OA为y=2x(x>0),射线OB为y= –2x(x>0),动点P(x, y)在 的内部,
的内部,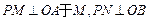 于N,四边形ONPM的面积为2..
于N,四边形ONPM的面积为2..
(I)动点P的纵坐标y是其横坐标x的函数,求这个函数y=f(x)的解析式;
(II)确定y=f(x)的定义域.
 |