已知抛物线的顶点在坐标原点 ,焦点
,焦点 在
在 轴上,抛物线上的点
轴上,抛物线上的点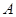 到
到 的距离为2,且
的距离为2,且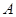 的横坐标为1.直线
的横坐标为1.直线 与抛物线交于
与抛物线交于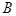 ,
,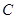 两点.
两点.
(1)求抛物线的方程;
(2)当直线 ,
,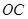 的倾斜角之和为
的倾斜角之和为 时,证明直线
时,证明直线 过定点.
过定点.
已知函数 是奇函数,
是奇函数,
(1)求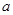 的值;
的值;
(2)若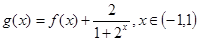 ,求
,求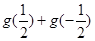 的值.
的值.
全集
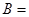

求集合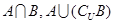 .
.
已知函数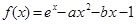 ,其中
,其中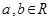 ,e=2.718 28 为自然对数的底数.
,e=2.718 28 为自然对数的底数.
(1)设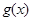 是函数
是函数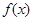 的导函数,求函数
的导函数,求函数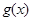 在区间
在区间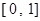 上的最小值;
上的最小值;
(2)若 ,函数
,函数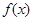 在区间
在区间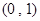 内有零点,证明:
内有零点,证明: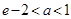 .
.
设椭圆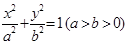 的左、右焦点分别为F1,F2,右顶点为A,上顶点为B.已知|AB|=
的左、右焦点分别为F1,F2,右顶点为A,上顶点为B.已知|AB|=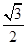 |F1F2|.
|F1F2|.
(1)求椭圆的离心率;
(2)设P为椭圆上异于其顶点的一点,以线段PB为直径的圆经过点F1,经过原点O的直线l与该圆相切,求直线l的斜率.
如图,在三棱柱 中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.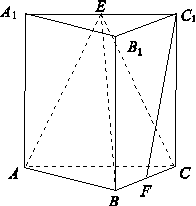
(1)求证:平面ABE⊥平面B1BCC1;
(2)求证:C1F∥平面ABE;
(3)求三棱锥E —ABC的体积.