如图，在三棱柱
中，侧棱垂直于底面，AB⊥BC，AA1＝AC＝2，BC＝1，E，F分别是A1C1，BC的中点．
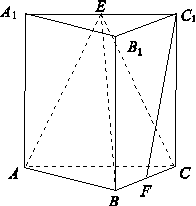
（1）求证：平面ABE⊥平面B1BCC1；
（2）求证：C1F∥平面ABE；
（3）求三棱锥E —ABC的体积.
已知
，
R
（Ⅰ）当
时，解不等式
；
（Ⅱ）若
恒成立，求k的取值范围.
已知直线
（t为参数）经过椭圆
（
为参数）的左焦点F.
（Ⅰ）求m的值；
（Ⅱ）设直线l与椭圆C交于A、B两点，求|FA|·|FB|的最大值和最小值.
如图所示，AC为
的直径，D为
的中点，E为BC的中点.
（Ⅰ）求证：AB∥DE；
（Ⅱ）求证：2AD·CD＝AC·BC.
已知动圆C经过点(0，m) (m>0)，且与直线y＝－m相切，圆C被x轴截得弦长的最小值为1，记该圆的圆心的轨迹为E.
（Ⅰ）求曲线E的方程；
（Ⅱ）是否存在曲线C与曲线E的一个公共点，使它们在该点处有相同的切线？若存在，求出切线方程；若不存在，说明理由.
已知函数
（Ⅰ）若
在（0，
）单调递减，求a的最小值
（Ⅱ）若有两个极值点，求a的取值范围.