已知函数
(Ⅰ)若 在(0,
在(0, )单调递减,求a的最小值
)单调递减,求a的最小值
(Ⅱ)若 有两个极值点,求a的取值范围.
有两个极值点,求a的取值范围.
已知lgx+lgy=2 lg(2x-3y),求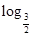
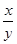 的值.
的值.
定义在[-1,1]上的奇函数f(x),已知当x∈[-1,0]时,
f(x)=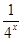 -
-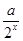 (a∈R).
(a∈R).
(1)求f(x)在[0,1]上的最大值;
(2)若f(x)是[0,1]上的增函数,求实数a的取值范围.
已知函数f(x)=2x,g(x)= +2.
+2.
(1)求函数g(x)的值域;
(2)求满足方程f(x)-g(x)=0的x的值.
已知函数y=2-x2+ax+1在区间(-∞,3)内递增,求a的取值范围.
对于函数f(x)若存在x0∈R,f(x0)=x0成立,则称x0为f(x)的不动点.已知f(x)=ax2+(b+1)x+b-1(a≠0).
(1)当a=1,b=-2时,求函数f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上A,B两点的横坐标是函数f(x)的不动点,且A,B两点关于直线y=kx+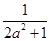 对称,求b的最小值.
对称,求b的最小值.