已知地球半径为R,地球表面重力加速度为g,万有引力常量为G,不考虑地球自转的影响。
(1)求卫星环绕地球运行的第一宇宙速度v1;
(2)若卫星绕地球做匀速圆周运动且运行周期为T,求卫星运行半径r;
(3)由题目所给条件,请提出一种估算地不堪平均密度的方法,并推导出密度表达式。
因测试需要,一辆汽车在某雷达测速区,沿平直路面从静止开始匀加速一段时间后,又接着做匀减速运动直到最后停止.下表中给出了雷达测出的各个时刻对应的汽车速度数值.求:
(1)汽车匀加速和匀减速两阶段的加速度a1、a2分别是多大?
(2)汽车在该区域行驶的总位移x是多少?
| 时刻/s |
0 |
1.0 |
2.0 |
3.0 |
4.0 |
5.0 |
6.0 |
7.0 |
8.0 |
9.0 |
10.0 |
| 速度/ m·s-1 |
0 |
3.0 |
6.0 |
9.0 |
12.0 |
10.0 |
8.0 |
6.0 |
4.0 |
2.0 |
0 |
一辆卡车初速度为v0=10m/s,以a=2m/s2的加速度行驶,求:
(1)卡车在3s末的速度v
(2)卡车在6s内的位移x6与平均速度
(3)卡车在第6s内的位移xⅥ
在倾角为θ的斜坡上,某同学骑在自行车上,刚好能在不踩踏板的情况下使自行车沿斜坡匀速向下行驶。现在他骑着自行车以某一速度沿此斜坡匀速上行,已知在t时间内,他踩着脚蹬板转了N圈(不间断地匀速蹬),又已知自行车和人的总质量为m,自行车链轮的半径为R1,飞轮的半径为R2,后车轮的半径为R3,设上、下坡过程中斜坡及空气作用于自行车的阻力大小相等,车轮与坡面接触处都无滑动(提示:自行车行驶的速度等于后轮边缘一点相对于轴心转动的线速度大小),不计自行车内部各部件之间因相对运动而消耗的能量。求人骑自行车上坡时的功率。
如图1所示,A和B是真空中两块面积很大的平行金属板、加上交变电压,在两板间产生变化的电场。已知B板电势为零,在0~T时间内,A板电势UA随时间变化的规律如图2所示,其中UA的最大值为U0,最小值为 -2U0 。在图1中,虚线MN表示与A、B板平行且等距的一个较小的面,此面到A和B的距离皆为L。在此面所在处,不断地产生电量为q、质量为m的带负电微粒,微粒随时间均匀产生出来。微粒产生后,从静止出发在电场力的作用下运动。设微粒一旦碰到金属板,就附在板上不再运动,且其电量同时消失,不影响A、B板的电压。已知在0~T时间内产生出来的微粒,最终有四分之一到达了A板,求这种微粒的比荷(q/m)。(不计微粒重力,不考虑微粒之间的相互作用)。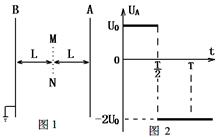
如图所示,质量M =10kg,倾角θ =37°的斜面体静止在粗糙的水平地面上,斜面体和水平面间的动摩擦因数µ =0.04。一质量m =2kg的物体由静止开始沿斜面下滑,沿斜面下滑2m时物体的速度为v =2m/s,此过程中,斜面体一直处于静止状态。求: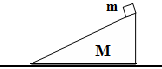
(1)地面对斜面体的摩擦力大小;
(2)地面对斜面体的支持力大小。