（本小题满分13分）
一个袋中装有
个形状大小完全相同的小球，球的编号分别为
.
（Ⅰ）若从袋中每次随机抽取1个球，有放回的抽取2次，求取出的两个球编号之和为6的概率；
（Ⅱ）若从袋中每次随机抽取
个球，有放回的抽取3次，求恰有次抽到号球的概率；
（Ⅲ）若一次从袋中随机抽取
个球，记球的最大编号为
，求随机变量的分布列.
（本小题12分）已知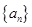
是等差数列，其中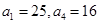
（1）求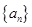的通项公式；
（2）数列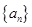从哪一项开始小于0。
某学校共有教职工900人，分成三个批次进行继续教育培训，在三个批次中男、女教职工人数如下表所示．已知在全体教职工中随机抽取1名，抽到第二批次中女教职工的概率是0．16 ．
| 第一批 |
第二批 |
第三批 |
|
| 女 |
196 |
x |
y |
| 男 |
204 |
156 |
z |
（1）求
的值；
（2）现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查，问应在第三批次中抽取教职工多少名？
（3）已知
，求第三批次中女教职工比男教职工多的概率．
某校高三某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如下图，据此解答如下问题：
（1）求分数在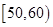
的频率及全班的人数；
（2）求分数在
之间的频数，并计算频率分布直方图中间的矩形的高；
（3）若要从分数在
之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份在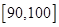
之间的概率。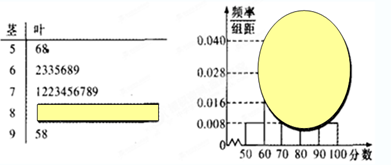
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量
（吨）与相应的生产能耗
（吨标准煤）的几组对照数据
|
3 |
4 |
5 |
6 |
|
2．5 |
3 |
4 |
4．5 |
（
）
（1）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程
；
（2）已知该厂技术改造前１００吨甲产品能耗为９０吨标准煤．试根据（1）求出的线性回归方程，预测生产１００吨甲产品的生产能耗比技术改造前降低多少吨标准煤？
某校从参加科普知识竞赛的学生中抽出60名学生，将其成绩（均为整数）分成六段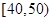
，
，……，
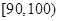后画出如右的部分频率分布直方图，观察图形的信息，回答下列问题：
（1）求第四段的频率，并补全这个频率分布直方图；
（2）求这次考试的及格率（60分以上为及格）；
（3）求这60名孩子的平均分