(本小题满分14分)已知锐角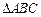 中的三个内角分别为
中的三个内角分别为 .
.
(1)设·=·,求证: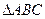 是等腰三角形;
是等腰三角形;
(2)设向量=(2sinC, -), =(cos2C, 2cos2 -1), 且∥, 若sinA=,求sin(-B)的值.
已知函数f (x) =" ln" (2 + 3x) 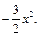
(1)求f (x)在[0,1]上的最大值;
(2)若对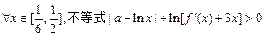 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若关于x的方程f (x) = –2x + b在[0,1]上恰有两个不同的实根,求实数b的取值范围.
设直线 . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.
⑴已知函数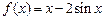 .求证:
.求证: 为曲线
为曲线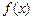 的“上夹线”.
的“上夹线”.
⑵观察下图: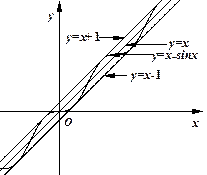
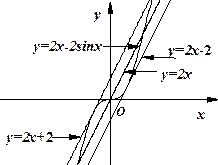
根据上图,试推测曲线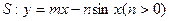 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.
某地需要修建一条大型输油管道通过120公里宽的沙漠地带,该段输油管道两端的输油站已建好,余下工程只需要在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站(又称泵站).经预算,修建一个增压站的工程费用为432万元,铺设距离为 公里的相邻两增压站之间的输油管道费用为
公里的相邻两增压站之间的输油管道费用为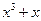 万元.设余下工程的总费用为
万元.设余下工程的总费用为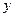 万元.
万元.
(Ⅰ)试将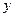 表示成关于
表示成关于 的函数;
的函数;
(Ⅱ)需要修建多少个增压站才能使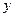 最小?
最小?
已知关于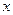 的不等式
的不等式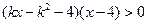 ,其中
,其中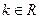 .
.
⑴当 变化时,试求不等式的解集
变化时,试求不等式的解集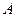 ;
;
⑵对于不等式的解集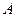 ,若满足
,若满足 (其中
(其中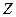 为整数集). 试探究集合
为整数集). 试探究集合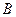 能否为有限集?若能,求出使得集合
能否为有限集?若能,求出使得集合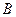 中元素个数最少的
中元素个数最少的 的所有取值,并用列举法表示集合
的所有取值,并用列举法表示集合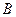 ;若不能,请说明理由.
;若不能,请说明理由.
已知函数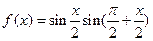
⑴求函数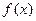 在[
在[ ]上的单调区间;
]上的单调区间;
⑵已知角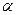 满足
满足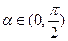 ,
,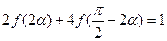 ,求
,求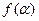 的值。
的值。