已知关于 的不等式
的不等式 ,其中
,其中
 。
。
(1)求上述不等式的解;
(2)是否存在实数 ,使得上述不等式的解集
,使得上述不等式的解集 中只有有限个整数?若存在
中只有有限个整数?若存在 ,求出使得
,求出使得 中整数个数最少的
中整数个数最少的 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(本小题9分)
如图,四棱锥S—ABCD的底面是正方形,SD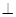 平面ABCD,SD=2a,
平面ABCD,SD=2a, ,点E是SD上的点,且
,点E是SD上的点,且

(Ⅰ)求证:对任意的 ,都有
,都有
(Ⅱ)设二面角C—AE—D的大小为
 ,直线BE与平面ABCD所成的角为
,直线BE与平面ABCD所成的角为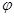 ,若
,若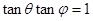 ,求
,求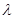 的值
的值
(本小题8分)
如图,点 为斜三棱柱
为斜三棱柱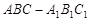 的侧棱
的侧棱 上一点,
上一点,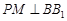 交
交 于点
于点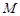 ,
, 交
交 于点
于点 .
.
(1) 求证: ;
;
(2) 在任意 中有余弦定理:
中有余弦定理: . 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式(只写结论,不必证明)
. 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式(只写结论,不必证明)
(本小题9分)
求函数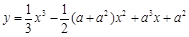 的单调递减区间.
的单调递减区间.
(本小题8分)
一个口袋内有4个不同的红球,6个不同的白球.
(1)从中任取4个球,红球的个数不比白球少的取法有多少种?
(2)若取一个红球记2分,取一个白球记1分,从中任取4个球,使总分不少于7分的取法有多少种?
为了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);……;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8.
(1)将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
(2)求调查中随机抽取了多少个学生的百米成绩;
(3)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.