为了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);……;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8.
(1)将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
(2)求调查中随机抽取了多少个学生的百米成绩;
(3)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.
已知函数
(Ⅰ)若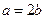 ,试问函数
,试问函数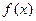 能否在
能否在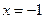 取到极值?若有可能,求出实数
取到极值?若有可能,求出实数 的值;否则说明理由.
的值;否则说明理由.
(Ⅱ)若函数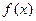 在区间(-1,2),(2,3)内各有一个极值点,试求
在区间(-1,2),(2,3)内各有一个极值点,试求 的取值范围.
的取值范围.
把一颗骰子投掷两次,第一次出现的点数记为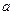 ,第二次出现的点数记为
,第二次出现的点数记为 ,试就方程组
,试就方程组 解答下列各题:
解答下列各题:
(Ⅰ)求方程组只有一组解的概率;
(Ⅱ)求方程组只有正数解的概率.
在△ABC中,三内角A、B、C及其对边a、b、c,满足sin(A-B)=sinB+sinC.
(Ⅰ)求角A的大小;
(Ⅱ)若a=6,求△ABC面积的最大值.
已知函数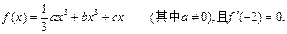
(1)若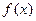 在x=2处取得极小值-2,求
在x=2处取得极小值-2,求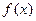 的单调区间;
的单调区间;
(2)令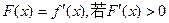 的解集是A,且A∪(0,1)=(-∞,1),求
的解集是A,且A∪(0,1)=(-∞,1),求 的最大值.
的最大值.
已知数列 中,a1=1,a2=3,且
中,a1=1,a2=3,且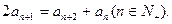 数列
数列 的前n项和为Sn,其中
的前n项和为Sn,其中
(1)求数列 和
和 的通项公式;
的通项公式;
(2)若 的表达式.
的表达式.