已知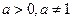 ,
, 设p:函数
设p:函数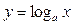 在
在 上单调递减,
上单调递减,
q:曲线y=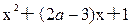 与x轴交于不同的两点.若“p且q”为假,“
与x轴交于不同的两点.若“p且q”为假,“ q”为
q”为
假,求 的取值范围
的取值范围
某部门对当地城乡居民进行了主题为“你幸福吗?”的幸福指数问卷调査,并在已被问卷调查的居民中随机抽选部分居民参加“幸福职业”或“幸福愿景”的座谈会,被邀请的居民只能选择其中一场座谈会参加.已知A小区有1人,B小区有3人收到邀请并将参加一场座谈会,若A小区已经收到邀请的人选择参加“幸福愿景”座谈会的概率是 , B小区已经收到邀请的人选择参加“幸福愿景”座谈会的概率是
, B小区已经收到邀请的人选择参加“幸福愿景”座谈会的概率是 .
.
(Ⅰ)求A、B两个小区已收到邀请的人选择“幸福愿景”座谈会的人数相等的概率;
(Ⅱ)在参加“幸福愿景”座谈会的人中,记A、B两个小区参会人数的和为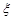 ,试求
,试求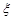 的分布列和数学期望.
的分布列和数学期望.
在锐角三角形ABC中,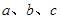 分别是角A、B、C的对边,且
分别是角A、B、C的对边,且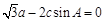 .
.
(Ⅰ)求角C的大小;
(Ⅱ)若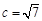 ,且△ABC 的面积为
,且△ABC 的面积为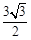 ,求
,求 的值.
的值.
设数列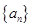 满足
满足
(I)求数列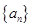 的通项公式;
的通项公式;
(II)设 求数列
求数列 的前
的前 项和
项和 .
.
在正项等比数列 中,
中, ,
,  .
.
(1) 求数列 的通项公式
的通项公式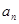 ;
;
(2) 记 ,求数列
,求数列 的前n项和
的前n项和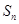 ;
;
(3) 记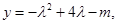 对于(2)中的
对于(2)中的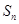 ,不等式
,不等式 对一切正整数n及任意实数
对一切正整数n及任意实数 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
如图,某动物园要建造两间完全相同的矩形熊猫居室,其总面积为24平方米,设熊猫居室的一面墙AD的长为x米  .
.
(1)用x表示墙AB的长;
(2)假设所建熊猫居室的墙壁造价(在墙壁高度一定的前提下)为每米1000元,请将墙壁的总造价y(元)表示为x(米)的函数;
(3)当x为何值时,墙壁的总造价最低?