椭圆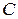 的方程为
的方程为 ,斜率为1的直线
,斜率为1的直线 与椭圆
与椭圆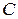 交于
交于 两点.
两点.
(Ⅰ)若椭圆的离心率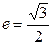 ,直线
,直线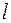 过点
过点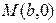 ,且
,且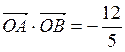 ,求椭圆
,求椭圆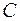 的方程;
的方程;
(Ⅱ)直线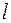 过椭圆的右焦点F,设向量
过椭圆的右焦点F,设向量 ,若点
,若点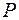 在椭圆
在椭圆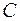 上,求
上,求 的取值范围.
的取值范围.
设椭圆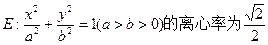 ,
,
已知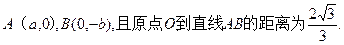
(Ⅰ)求椭圆E的方程;
(Ⅱ)已知过点M(1,0)的直线交椭圆E于C,D两点,若存在动点N,使得直线NC,NM,ND的斜率依次成等差数列,试确定点N的轨迹方程.
在直角梯形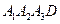 中,
中,
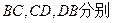 将
将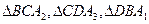 翻折上去恰好使
翻折上去恰好使

(Ⅰ) 求证: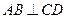 ;
;
(Ⅱ)已知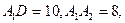 试求:
试求:
(1)四面体ABCD内切球的表面积;
(2)二面角 的余弦值.
的余弦值.
已知数列{an}满足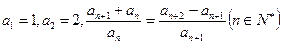
(Ⅰ) 试求a2011的值;
(Ⅱ)记数列 取值范围.
取值范围.
把函数 的图像上每一点的横坐标伸长到原来的2倍,纵坐标不变,然后再向左平移
的图像上每一点的横坐标伸长到原来的2倍,纵坐标不变,然后再向左平移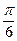 个单位后得到一个最小正周期为2
个单位后得到一个最小正周期为2 的奇函数
的奇函数 .
.
(Ⅰ) 求
 的值;
的值;
(Ⅱ) 的最大值与最小值.
的最大值与最小值.
(本小题满分10分)
如图,在y轴的正半轴上依次有点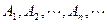 其中点
其中点 ,且
,且
 ,在射线
,在射线 上依次有
上依次有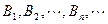 点
点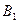 的坐
的坐 标为(3,3),且
标为(3,3),且


⑴用含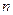 的式子表示
的式子表示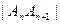 ;
;
⑵用含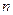 的式子表示
的式子表示 的坐标;
的坐标;
⑶求四边形 面积的最大值。
面积的最大值。