某校欲招聘一名数学教师,学校对甲、乙、丙三位候选人进行了三项能力测试,各项测试成绩满分均为100分,根据结果择优录用.三位候选人的各项测试成绩如下表所示:
| 测试项目 |
测试成绩 |
||
| 甲 |
乙 |
丙 |
|
| 教学能力 |
85 |
73 |
73 |
| 科研能力 |
70 |
71 |
65 |
| 组织能力 |
64 |
72 |
84 |
(1)如果根据三项测试的平均成绩,谁将被录用,说明理由;
(2)根据实际需要,学校将教学、科研和组织三项能力测试得分按5∶3∶2的比例确定每人的成绩,谁将被录用,说明理由
(本题8分)如图所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD,可以得到BD平分EF,为什么?说明理由.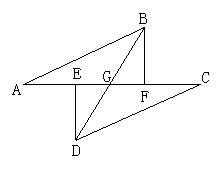
(本题8分)如图,△ABO≌△CDO,点B在CD上,AO∥CD,∠BOD=30°,求∠A的度数.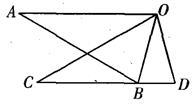
(本题7分)如图,点B、C在∠SAT的两边上,且AB=AC.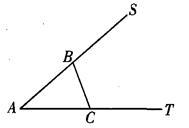
(1)请按下列语句用尺规画出图形.(不写画法,保留作图痕迹)
①AN⊥BC,垂足为N;
②∠SBC的平分线交AN延长线于点M;
③连接CM.
(2)该图中有_______对全等三角形.
(本题6分) 如图,在△ABC中,∠ACB=90,AC=BC.直线L经过点C且绕点C转动,分别过点A、B向直线DE引垂线,垂足分别为点D、E.
求证:AD+BE=DE.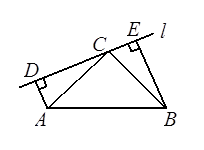
(本题6分)如图,点E、C在线段BF上,BE=CF,AB∥DE,∠ACB=∠F,那么△ABC与△DEF全等吗?为什么?